Beatrice的黄金魔法
会呼吸的金字塔
什么是金钱?
大多数自然人对金钱的理解来自于自身的经验(Karen Pryor赐予海豚的响片):小时候五毛钱的棒棒糖,现在十几块钱的一顿饭,大城市几千块钱的房租。
然而,仅从自然人的生活经验去理解金钱是非常片面的。
货币不是一个简单的实数,而是复杂的信用符号(symbol)金字塔
在添加时间维度之后,可以看到金字塔也是会呼吸(扩张/收缩)的,不同层级有不同的呼吸速度
1
2
3
4
5
6
7
风险金字塔:
T0 黄金
T1 霸权货币(美元)和利率债(美债)
T2 其余各国(即新兴市场)的主权货币和利率债
T3 优质(需求偏好稳定)垄断寡头企业
T4 其他现金流企业
T5 估值科创企业
自然人生活经验感知到的货币属于T1~T2(基础货币+信贷)
每一层级准备金率(reserve ratio)和杠杆率互相对应
参考:哥伦比亚大学《货币与银行经济学|Economics of Money and Banking》
主权货币
繁荣稳定时期T0黄金是无风险零息债券,定价参考T1实际利率
在T2接近零实际利率时风险极高,外汇汇率崩溃,应该持有T1
在T1接近零实际利率时风险极高,外汇汇率崩溃(此时黄金发挥货币属性), 应该持有T0(大周期的终结),例如2022年开始的美元计价黄金定价与实际利率背离
评估国家时应考虑四张表的负债率、财政赤字率、总杠杆、人口结构(主要是年龄如抚养比)
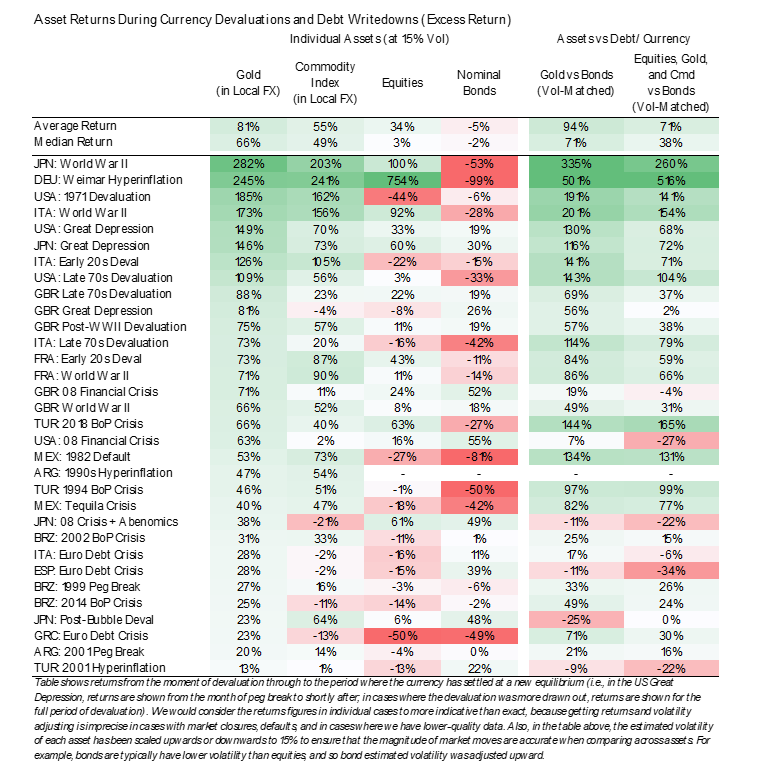
图: 主权货币在大周期的债务危机时会经历迅速贬值
利率曲线
利率不是一个数字,而是不同时间尺度的货币期货回报率,因此不同期限有不同的利率值,形成利率曲线,正常的利率曲线是近低远高(时间补偿,借短买长)
央行调控的是短端利率 核心目标是align通胀
3~6月期短债属于现金类资产
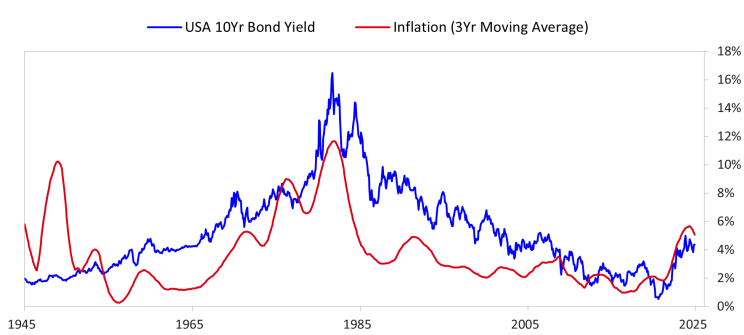
全社会企业盈利利率参考10年期国债收益率
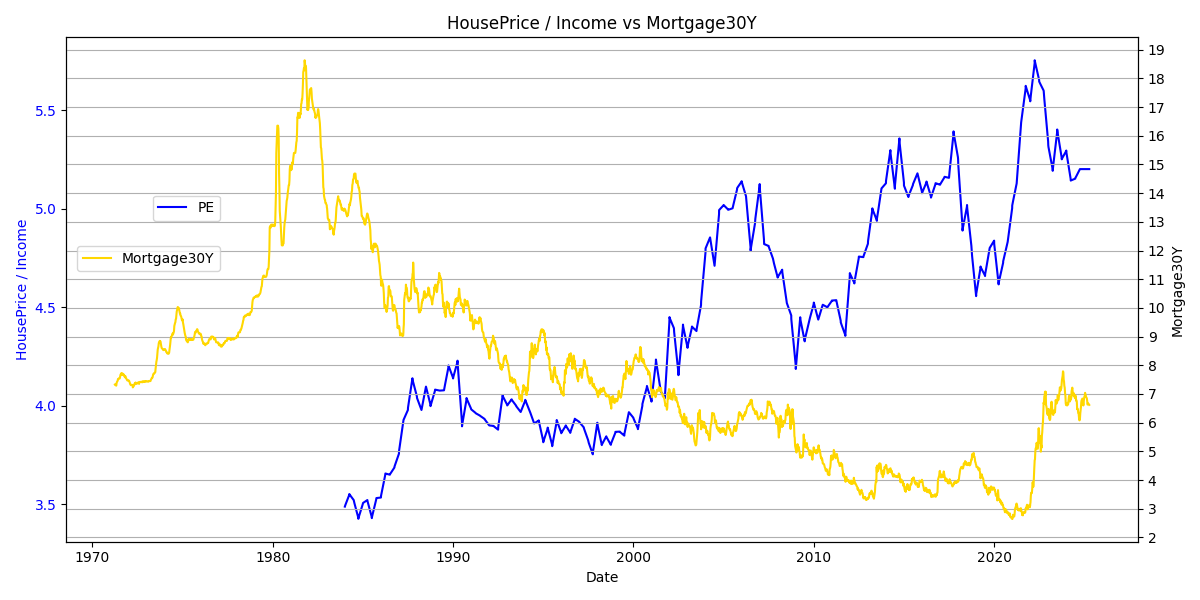
房地产参考30年期国债收益率
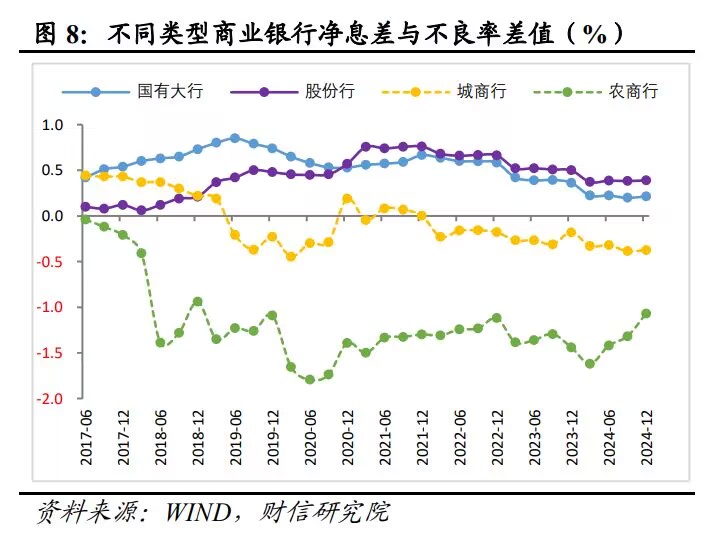
心理学经验:利率迅速降低时净息差迅速收缩(尚未到期的存款利率仍然很高,同时坏账率在上升,表现为小银行破产重组)
生活经验:10年期国债收益率长期低于3%时,应该格外提防各类诈骗(最可怕的是情感诈骗和金融产品诈骗,其最能hack大脑的动物情欲和贪婪)
金字塔的呼吸分为大周期(百年尺度)和数个小周期:
Ray Dalio: How The Economic Machine Works
企业
财政部(利率债发行主体)可以看作一个特殊的企业,其产出的商品是社会公共服务,收入来源主要是税收(所有国民即为员工)。
全社会企业盈利的baseline利率参考10年期国债收益率
秩序稳定时长期持有T1~T4,根据小周期扩张情况持有T5
评估企业要考虑供给需求(核心是远期的需求偏好)、forward PE、在产业链的位置、垄断能力、人口结构等等。
居民
居民收入参考 Median Household Income in the United States (MEHOINUSA646N)
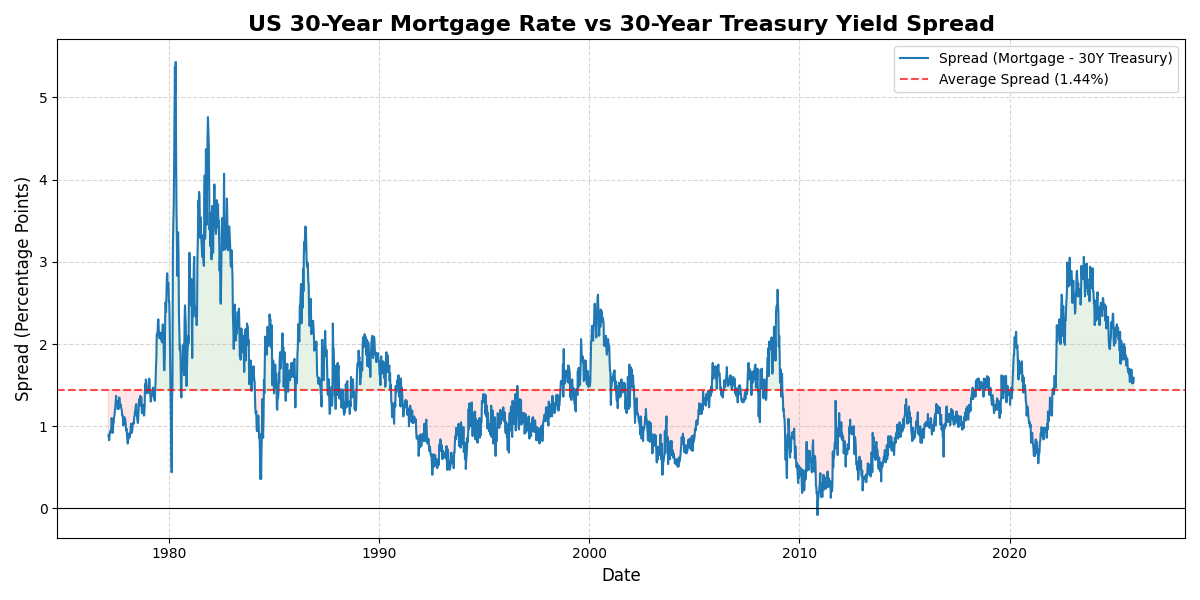
房地产参考30-Year Fixed Rate Mortgage Average in the United States (MORTGAGE30US)
Median Sales Price of Houses Sold for the United States (MSPUS)
Housing Inventory: Active Listing Count in the United States (ACTLISCOUUS)
美国2008次贷危机:
- 次贷是信用等级较次一级的客户
- 危机根源,gov创设房地美和房利美,设定目标希望大多数人能有住房,因此两家企业在03年后急剧扩大债权需求,创设浮动利率让尽可能多的人购买期房
- MBS导致的信息不对称: 资产持有主体不具有鉴别和筛选能力,发行机构没有利益动机保证评级诚实,加剧了逆向选择和道德风险
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
import pandas_datareader.data as web
import pandas as pd
import matplotlib.pyplot as plt
import datetime
start_date = datetime.datetime(1971, 4, 2)
end_date = datetime.datetime.now()
# FRED 数据系列 ID
# MORTGAGE30US: 30-Year Fixed Rate Mortgage Average in the United States (周频)
# DGS30: Market Yield on U.S. Treasury Securities at 30-Year Constant Maturity (日频)
series_ids = ['MORTGAGE30US', 'DGS30']
print("正在从 FRED 下载数据,请稍候...")
try:
# pandas_datareader 可以直接从 FRED 拉取数据
# 注意:如果你有 FRED API Key,可以使用 os.environ["FRED_API_KEY"] = "YOUR_KEY"
# 或者直接调用,通常少量数据不需要 Key 也能下载,如果失败请申请 Key。
df = web.DataReader(series_ids, 'fred', start_date, end_date)
# 因为国债是日频(Daily),房贷利率是周频(Weekly),数据会有空值(NaN)。
# 我们使用前向填充(ffill)来填补国债数据的空缺,以匹配房贷数据的发布日。
df['DGS30'] = df['DGS30'].ffill()
# 删除 'MORTGAGE30US' 为空的行(只保留房贷利率发布的那些日期)
df = df.dropna(subset=['MORTGAGE30US'])
df['Spread'] = df['MORTGAGE30US'] - df['DGS30']
# ---绘图 ---
plt.figure(figsize=(12, 6))
# 绘制利差线
plt.plot(df.index, df['Spread'], label='Spread (Mortgage - 30Y Treasury)', color='#1f77b4', linewidth=1.5)
# 添加平均值线作为参考
avg_spread = df['Spread'].mean()
plt.axhline(y=avg_spread, color='r', linestyle='--', alpha=0.7, label=f'Average Spread ({avg_spread:.2f}%)')
# 添加 0 轴线
plt.axhline(y=0, color='black', linewidth=0.8)
# 图表装饰
plt.title('US 30-Year Mortgage Rate vs 30-Year Treasury Yield Spread', fontsize=16, fontweight='bold')
plt.ylabel('Spread (Percentage Points)', fontsize=12)
plt.xlabel('Date', fontsize=12)
plt.legend(loc='upper right')
plt.grid(True, which='both', linestyle='--', alpha=0.5)
# 填充颜色,强调利差扩大的区域
plt.fill_between(df.index, df['Spread'], avg_spread, where=(df['Spread'] > avg_spread),
interpolate=True, color='green', alpha=0.1, label='Above Average')
plt.fill_between(df.index, df['Spread'], avg_spread, where=(df['Spread'] <= avg_spread),
interpolate=True, color='red', alpha=0.1, label='Below Average')
plt.tight_layout()
plt.savefig("US_house_spread.png")
# 打印最新数据
latest = df.iloc[-1]
print(f"最新日期: {latest.name.date()}")
print(f"房贷利率: {latest['MORTGAGE30US']}%")
print(f"30年美债: {latest['DGS30']}%")
print(f"当前利差: {latest['Spread']:.2f}%")
except Exception as e:
print(f"发生错误: {e}")
print("提示: 如果遇到网络错误,可能需要配置代理或申请 FRED API Key。")
将房产视为一种产生永续现金流的资产。
\[P = \frac{NOI}{Cap Rate} = \frac{R \times 12 \times (1 - V) \times (1 - M)}{r_f + L + T - g}\]- 基础月租金 (R): 30 元/平米。
- 空置率 (V): 10% —— 反映了摩擦性空置及市场供需错配风险
- 运营成本率 (M): 15% —— 涵盖物业费、交易税费、取暖费、中介佣金、保险及房屋维修基金摊销
- 无风险利率 (r_f): 2.1% —— 锚定 30年期国债收益率
- 流动性溢价 (L): 2%~4% —— 相对于无风险利率的溢价
- 房产税 (T): 0% —— 暂不考虑持有环节税收
- k: 1.25 —— 城市标度律, 这意味着人口每增长 1%,由于集聚效应带来的生产率提升,将推动内生性租金(及预期收入)增长 1.25%
根据REITs的数据,资本化率-30年期国债收益率:
- 一线城市 核心区域(深圳南山区)最低1.5%, 一般区域2%
- 二线城市 核心区域最低2.2%, 一般区域3%
工具 & 数据库
OpenBB Community Projects - FinanceToolkit
OpenBB Community Projects - FinanceDatabase
Yahoo Finance
Google Finance
Wind
Bloomberg
OpenBB
demo: 标普500 vs 利差金字塔
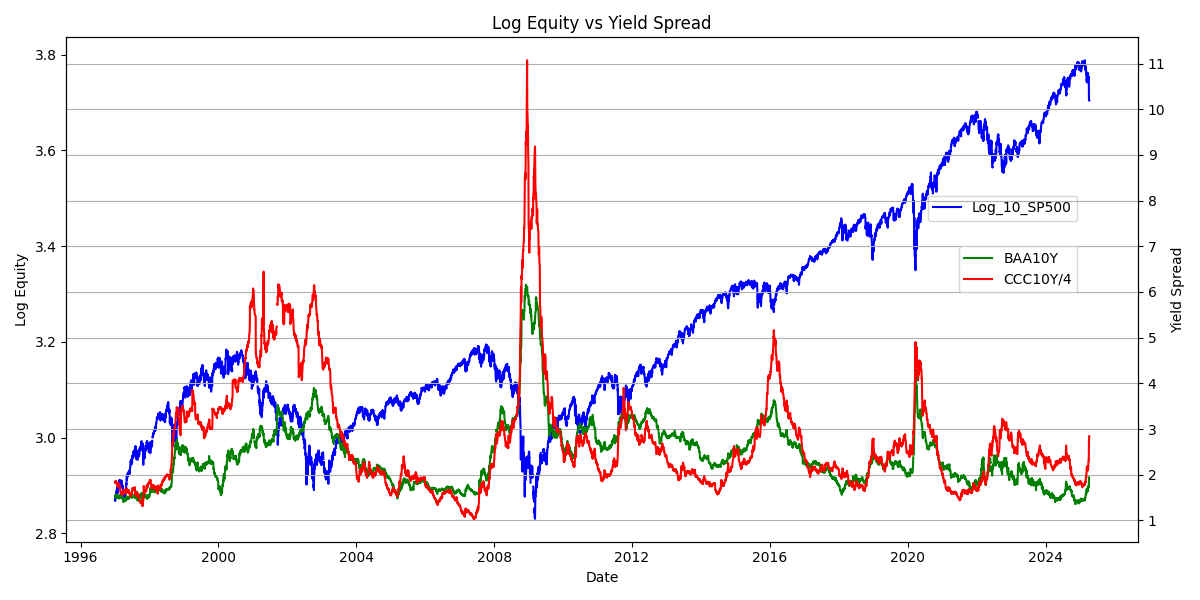
美债10年期收益率 - 3月期收益率反映了实际利率(更准确的指标应该是减去通胀),位于信用金字塔的T0~T1级别,对应美元信用;
BAA收益率溢价(经过期权调整)(baseline是十年期美债收益率)对应的是优质企业贷款需要付出的额外溢价,位于金字塔的T3和T4级别;
CCC收益率溢价(经过期权调整)(baseline是十年期美债收益率)对应的是普通企业贷款需要付出的额外溢价,位于金字塔的T5级别,其利率较低时意味着金字塔底端的资产也被大量的买入,整个金字塔接近扩张极限。
1
2
pip install openbb
pip install openbb-fred
标普500的数据来源Yahoo Finance 不需要api
CCC垃圾级债券收益率溢价BAMLH0A3HYC的数据来源fred需要申请api
申请理由参考:
1
I am a student working on an economic analysis project and need access to various economic data sets for research purposes.
本地创建config.yaml
1
fred_api_key: "xxx"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
import yaml
from openbb import obb
import numpy as np
from datetime import datetime
import os
# 读取config.yaml中的API key
with open("config.yaml", "r") as file:
config = yaml.safe_load(file)
fred_api_key = config.get("fred_api_key", "")
obb.user.credentials.fred_api_key = fred_api_key # 设置 FRED API key
# 获取起止日期
end_date = datetime.today().strftime("%Y-%m-%d")
start_date = "1996-12-31"
cache_folder = "data_cache" # 设置缓存文件夹
if not os.path.exists(cache_folder):
os.makedirs(cache_folder)
# 从缓存加载数据,如果缓存文件不存在则下载并缓存
def load_data_from_cache_or_download(sym, s_date, e_date, data_type="fred"):
# 生成缓存文件名
def get_cache_filename(symbol, start_date, end_date):
return os.path.join(cache_folder, f"{symbol}_{start_date}_{end_date}.csv")
cache_filename = get_cache_filename(sym, s_date, e_date)
# 如果缓存文件存在,则直接加载
if os.path.exists(cache_filename):
print(f"Loading {sym} data from cache: {cache_filename}")
return pd.read_csv(cache_filename, index_col=0, parse_dates=True)
# 如果缓存文件不存在,则下载数据
if data_type == "fred":
data = obb.economy.fred_series(symbol=sym, start_date=s_date, end_date=e_date).to_df()
data = data.rename(columns={"value": sym})
elif data_type == "yfinance":
data = obb.equity.price.historical(symbol=sym, start_date=s_date, end_date=e_date, provider="yfinance").to_df()
data = data.rename(columns={"close": sym})
# 保存数据到缓存
print(f"save {sym} data to cache: {cache_filename}")
data.to_csv(cache_filename)
return data
# 获取 fred数据 实际利率 企业债利差(BAA & CCC)
T10Y3M_data = load_data_from_cache_or_download("T10Y3M", start_date, end_date, data_type="fred")
BAA_data = load_data_from_cache_or_download("BAA10Y", start_date, end_date, data_type="fred")
CCC_data = load_data_from_cache_or_download("BAMLH0A3HYC", start_date, end_date, data_type="fred")
# 获取 yfinance数据 标普500数据
sp500_data = load_data_from_cache_or_download("^GSPC", start_date, end_date, data_type="yfinance")
merged_data = pd.DataFrame(
{
"T10Y3M": T10Y3M_data["T10Y3M"], # 美债10y-3m 实际利率
"BAA10Y": BAA_data["BAA10Y"], # BAA级债券利差 穆迪
"BAMLH0A3HYC": CCC_data["BAMLH0A3HYC"], # CCC级债券利差 ICE BofA
"Log_10_SP500": np.log10(sp500_data["^GSPC"]), # 标普500对数值
}
)
# .dropna() # 去除缺失值(如果有)
# 绘制双轴图
fig, ax1 = plt.subplots(figsize=(12, 6))
# 在主轴上绘制 Log_10_SP500
ax1.plot(merged_data.index, merged_data["Log_10_SP500"], color="blue", label="Log_10_SP500")
ax1.set_xlabel("Date")
ax1.set_ylabel("Log of SP500 Index", color="blue")
ax1.tick_params(axis="y", labelcolor="blue")
# 创建第二个Y轴,用于绘制 BAA10Y 和 BAMLH0A3HYC
ax2 = ax1.twinx()
ax2.yaxis.set_major_locator(MultipleLocator(1)) # 刻度间隔为1
(line1,) = ax2.plot(merged_data.index, merged_data["T10Y3M"], color="orange", label="10Y-3M")
(line2,) = ax2.plot(merged_data.index, merged_data["BAA10Y"], color="green", label="BAA")
(line3,) = ax2.plot(merged_data.index, merged_data["BAMLH0A3HYC"] / 4, color="red", label="CCC / 4")
ax2.set_ylabel("Yield Spread (%)", color="black") # 使用黑色表示次轴的标签
ax2.tick_params(axis="y", labelcolor="black")
# 添加标题和图例
plt.title("Log_10_SP500 vs Yield Spreads (10Y-3M & BAA & CCC/4)")
# 手动创建图例
lines = [line1, line2, line3] # 获取第二个 Y 轴的线条对象
labels = [line.get_label() for line in lines] # 获取对应的标签
ax2.legend(lines, labels, loc="upper right", bbox_to_anchor=(0.95, 0.63)) # 图例放在左上角
# 主轴的图例
ax1.legend(loc="upper right", bbox_to_anchor=(0.95, 0.70)) # 图例放在右上角
plt.grid(True)
plt.tight_layout()
plt.savefig("Log_SP500_vs_Yield_Spreads.png")
# 输出基本统计信息
print("\n基本统计信息:")
print(merged_data.describe())
def percentile_today(data, name):
today = data.iloc[-1][name] # 最新数据点
p = (data < today).mean()[name] * 100
print(f"{name}, {today}%, {p:.2f}%")
print("\nSymbol, 今日利差, 历史百分位")
percentile_today(T10Y3M_data, "T10Y3M")
percentile_today(BAA_data, "BAA10Y")
percentile_today(CCC_data, "BAMLH0A3HYC")
运行结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
基本统计信息:
T10Y3M BAA10Y BAMLH0A3HYC Log_10_SP500
count 7071.000000 7065.000000 7379.000000 7112.000000
mean 1.349574 2.429023 11.069318 3.240964
std 1.295788 0.736006 5.111355 0.232533
min -1.890000 1.360000 4.140000 2.830287
25% 0.380000 1.870000 7.690000 3.064991
50% 1.420000 2.290000 9.530000 3.151180
75% 2.350000 2.850000 12.595000 3.422043
max 3.850000 6.160000 44.290000 3.788462
Symbol, 2025-03-05利差, 历史百分位
T10Y3M, -0.07%, 13.59%
BAA10Y, 1.57%, 6.62%
BAMLH0A3HYC, 7.74%, 25.68%
Symbol, 2025-04-09利差, 历史百分位
T10Y3M, -0.14%, 12.80%
BAA10Y, 1.94%, 28.38%
BAMLH0A3HYC, 11.37%, 66.09%
从2025-03-05三者的历史百分位可以看出,均位于历史低位,意味着金字塔接近扩张极限,杠杆率极高
到2025-04-09三者的历史百分位变化可以看出,去杠杆收缩时金字塔底部先迅速爆掉,风险偏好逐步向金字塔顶端收缩
1
2
3
卖出信号(30%分位):CCC < 8% || BAA < 2%
买入信号(80%分位):CCC > 14% && BAA > 3%
分批操作
CCC位于金字塔 企业层级中的最低层次,主要用于风险提醒(是最后能加的杠杆)
BAA位于金字塔 企业层级中的较上层次,标普500更应该参考此指标
实际利率位于金字塔的T1层次,由于:
- 黄金可以看作零息债券 且 地表数量有限
- 实际利率触及0时 美债收益率无竞争优势
- 实际利率触及0时 美债数量不可控(若同时债务占GDP较高, 没有太多货币政策空间)
因此此时T1美元信用迅速下降,黄金将迎来大的上涨
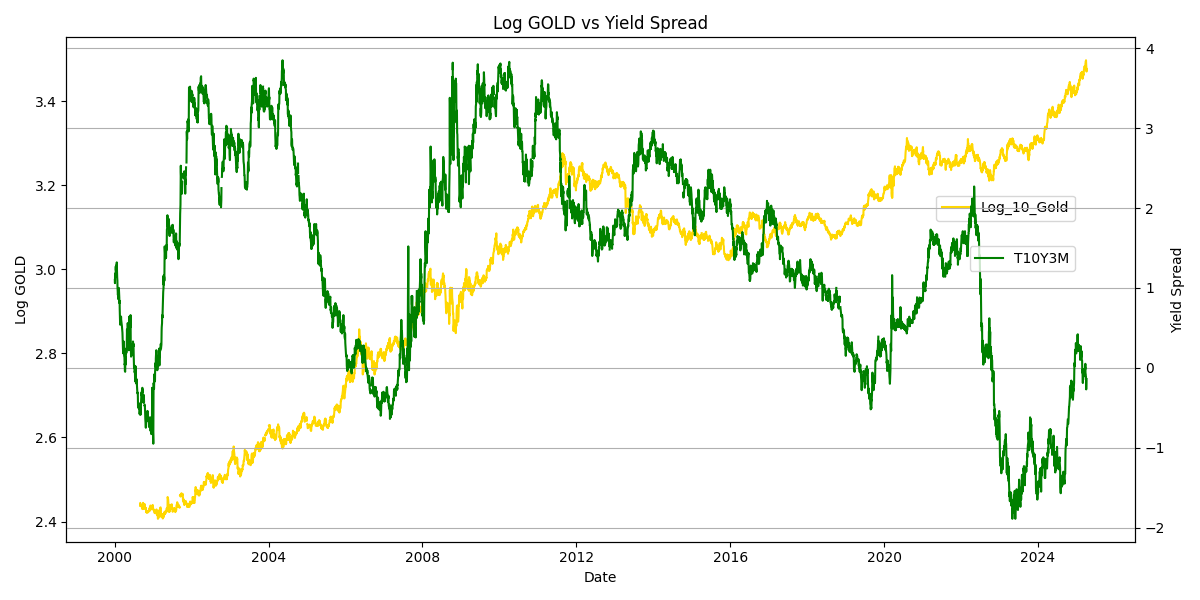
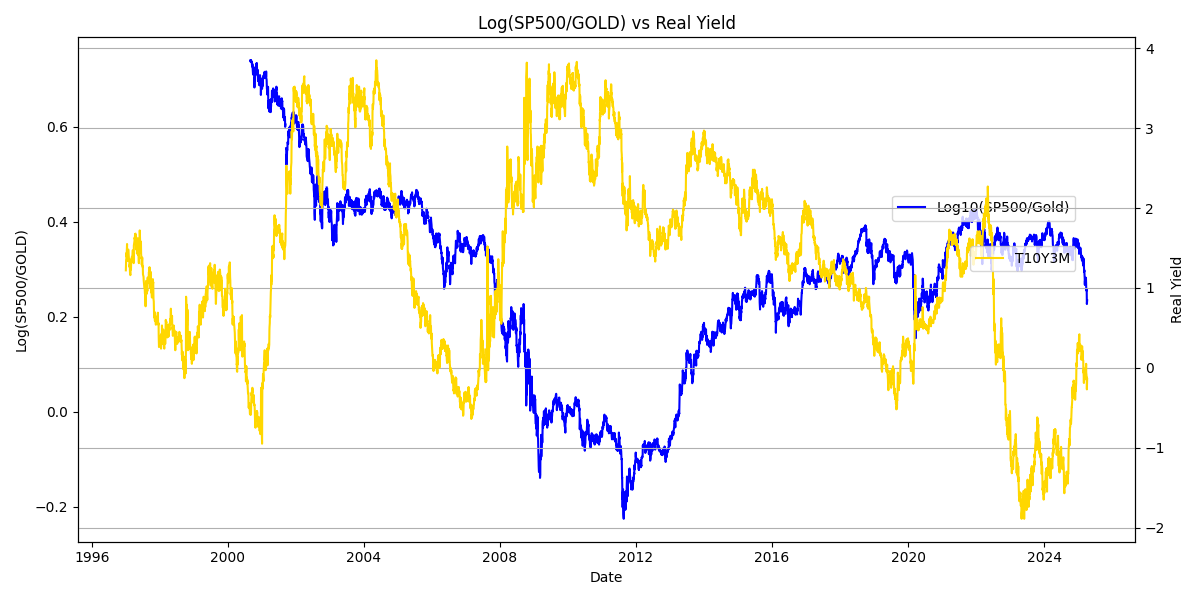
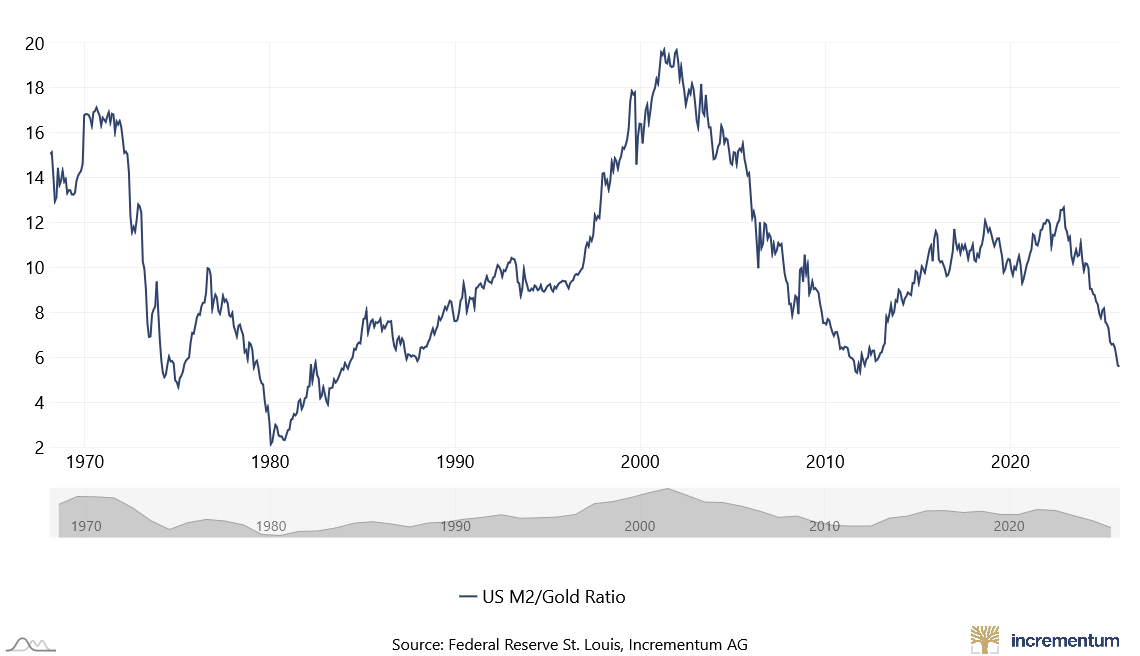
黄金计价的美股log10(sp500/gold)
The chart shows US M2 money supply in billions of US dollars (USD) divided by the price per ounce of gold in US dollars (USD) since 1968.
CLI
1
2
pip install openbb-cli
openbb
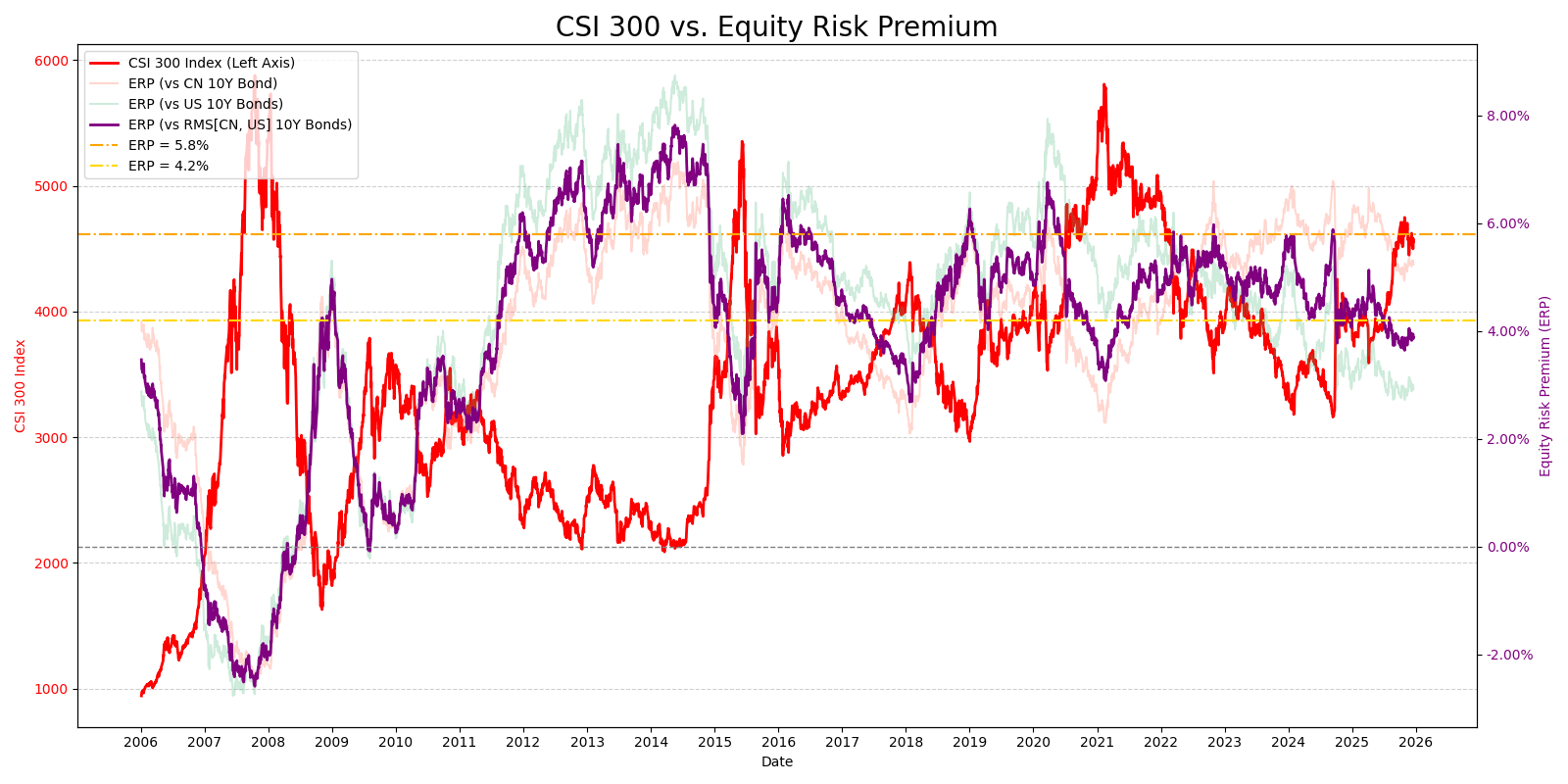
a-share
也要考虑年龄结构(老龄化)对风险偏好的影响
现有指标
ICE BofA CCC & Lower US High Yield Index Option-Adjusted Spread (BAMLH0A3HYC)
The Buffett Indicator: Market Cap to GDP
Gold vs. (inverted) Real 10-Year Treasury Yield
消费贷款: 可以是有抵押贷款(如汽车贷款以汽车为抵押,房屋净值贷款以房屋为抵押),也可以是无抵押贷款(如个人无抵押贷款、学生贷款)。有抵押的贷款通常利率较低,因为对贷款人风险较低。
信用卡贷款: 绝大多数信用卡贷款都是无抵押贷款,这意味着银行没有特定的资产作为担保。正因如此,信用卡贷款的利率通常较高。
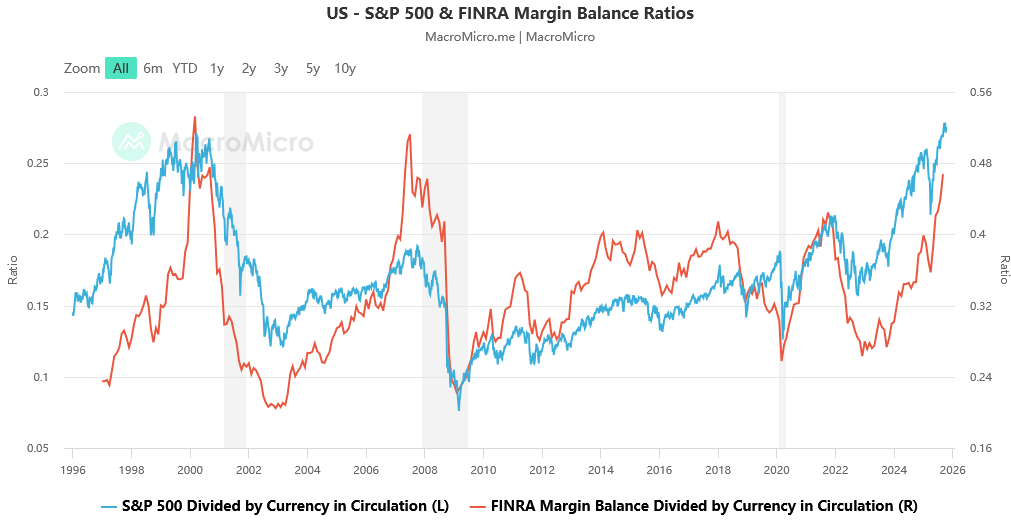
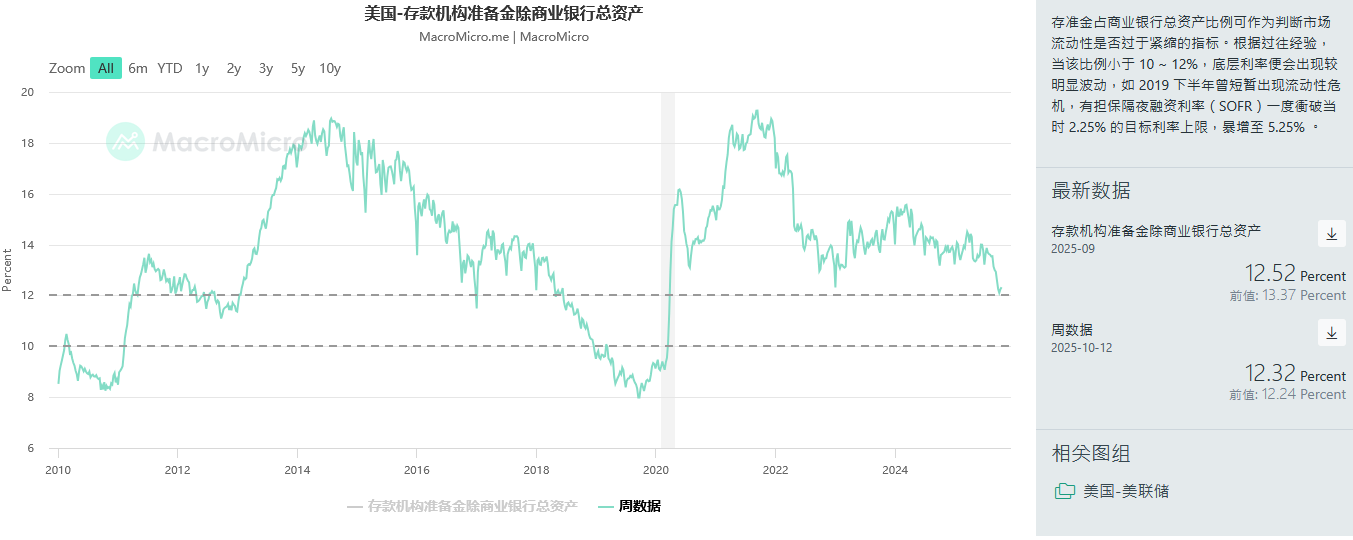
美国货币乘数 现象:85年后 美国和日本的货币乘数全部长期走低
FINRA Margin Balance Divided by Currency in Circulation (R) Margin Statistics Currency in Circulation (CURRCIR)
橙线:杠杆资金占比
三大评级机构: 穆迪 标普 惠誉
他者
神秘预测市场(zero-sum水晶球, 部分信息可以当作有相应造假成本的新闻看)
数字化Beatrice
部分科技爱好者打算将黄金魔女从Au197过渡到[算力~公私钥密码学]混合体
目前受众主体:按年龄切片划分,集中在z世代
TBD
财富分布
第一部分:基准模型 —— 无相互作用的“理想气体”社会
1. 基本假设与类比
将统计物理与社会经济学建立如下对应关系:
| 统计物理概念 | 社会经济学类比 | 解释 |
|---|---|---|
| 粒子 (Particles) | 个人 (Individuals) | 构成系统的基本单元。 |
| 总粒子数 $N$ | 总人口 $N$ | 假设1: 人口守恒,$N$ 为常数。 |
| 能量 ($E$) | 财富 ($W$) | 个人之间可以交换的量。 |
| 总能量 ($E_{\text{total}}$) | 总财富 ($W_{\text{total}}$) | 假设2: 财富守恒,$W_{\text{total}}$ 为常数(封闭系统)。 |
| 能量交换 | 经济交易/交换 | 假设3: 存在交换,个人财富发生转移。 |
| 能量级 ($\varepsilon_i$) | 财富水平 ($w_i$) | 个人可能拥有的离散财富数量。 |
| 宏观状态 | 整体财富分布 ${n_0, n_1, n_2, \dots}$ | 关心有多少人 ($n_i$) 处于各个财富水平 ($w_i$)。 |
| 微观状态 | 具体的财富分配 | 指明每一个特定的人拥有多少财富。 |
| 热平衡 | 社会经济稳定状态 | 经过大量交换后,系统达到的最可能、最稳定的财富分布。 |
| 熵 ($S$) | 社会可能性/多样性 | 对应一个宏观分布的微观分配方式的总数。 |
2. 最大熵原理
寻求使熵 $S = k \ln \Omega$ 最大的宏观状态 ${n_i}$,其中 $\Omega$ 是微观状态数。
系统的约束条件:
- 人口守恒:
\(\sum_{i} n_i = N\) - 财富守恒:
\(\sum_{i} n_i w_i = W_{\text{total}}\)
熵的表达(微观状态数):
对于 $N$ 个可区分个体分配到各财富等级:
\[\Omega(n_0, n_1, \dots) = \frac{N!}{\prod_{i} n_i!}\]使用斯特林近似 $\ln(x!) \approx x \ln x - x$,得:
\[\ln \Omega \approx N \ln N - \sum_i n_i \ln n_i\]构造拉格朗日函数:
\[L = \left(N\ln N - \sum_i n_i \ln n_i\right) - \alpha\left(\sum_i n_i - N\right) - \beta\left(\sum_i n_i w_i - W_{\text{total}}\right)\]对 $n_k$ 求偏导并令为零:
\[\frac{\partial L}{\partial n_k} = -(\ln n_k + 1) - \alpha - \beta w_k = 0 \Rightarrow \ln n_k = -1 - \alpha - \beta w_k\]从而得到:
\[n_k = C \cdot e^{-\beta w_k}, \quad \text{其中 } C = e^{-1 - \alpha}\]得到玻尔兹曼分布:拥有财富 $w_k$ 的人数随财富呈指数衰减。
3. 基尼系数
将分布连续化为概率密度函数: \(P(w) = A \cdot e^{-\beta w}\)
归一化:
\[\int_0^\infty P(w)\, dw = 1 \Rightarrow A = \beta \Rightarrow P(w) = \beta e^{-\beta w}\]该分布的均值(即“社会经济温度”)为: \(\langle w \rangle = \int_0^\infty w \beta e^{-\beta w} dw = \frac{1}{\beta} \Rightarrow \beta = \frac{1}{\langle w \rangle} = \frac{1}{\Theta}\)
洛伦兹曲线 $L(x)$:
人口累积比例: \(x(w) = \int_0^w P(w') dw' = 1 - e^{-\beta w}\)
财富累积比例: \(L(w) = \frac{1}{\langle w \rangle} \int_0^w w' P(w') dw' = \beta^2 \int_0^w w' e^{-\beta w'} dw'\)
计算积分后得: \(L(w) = 1 - (1 + \beta w) e^{-\beta w}\)
将 $x = 1 - e^{-\beta w} \Rightarrow \beta w = -\ln(1 - x)$ 代入: \(L(x) = x + (1 - x)\ln(1 - x)\)
基尼系数:
\[G = 1 - 2 \int_0^1 L(x)\, dx = 1 - 2 \int_0^1 \left[ x + (1 - x)\ln(1 - x) \right] dx\]分别计算:
- $\int_0^1 x\, dx = \frac{1}{2}$
- $\int_0^1 (1 - x)\ln(1 - x)\, dx = -\frac{1}{4}$
因此: \(G = 1 - 2 \left( \frac{1}{2} - \frac{1}{4} \right) = 1 - \frac{1}{2} = 0.5\)
结论:在完全随机交换的理想社会中,财富分布为指数分布,对应的基尼系数为 0.5,这是财富不平等的基线。
第二部分:拓展模型 —— 引入社会交换相互作用的量子社会
引入社会相互作用修正个体的“有效财富”: \(W' = W + J_{\text{social}}\) 并假设概率分布形式仍为 $P(W) \propto e^{-W’/\Theta}$。
模型 2A:费米子社会(竞争与排斥)
假设:竞争排斥。相似财富水平人口越多,维持该状态成本越高(内卷): \(J_{\text{social}} = \alpha \rho(W), \quad \alpha > 0,\quad \rho(W) = N P(W)\)
有效财富: \(W'(W) = W + \alpha N P(W)\)
自洽方程: \(P(W) = A \cdot e^{-(W + \alpha N P(W))/\Theta} \Rightarrow P(W) e^{\frac{\alpha N}{\Theta} P(W)} = A e^{-W/\Theta}\)
令 $k = \frac{\alpha N}{\Theta} > 0$,左边为 $f(P) = P e^{kP}$,单调递增。
- 抑制效应:由于 $e^{kP} \geq 1$,故 $P(W) \leq A e^{-W/\Theta}$,即分布处处低于经典玻尔兹曼形式。
- 中产“内卷”:在 $P(W)$ 较大的中等财富区域,抑制效应最强,分布被压平,财富增长困难。
社会学解释:竞争排斥导致阶层间流动性降低,中产阶级陷入红海博弈。
模型 2B:玻色子社会(合作与凝聚)
假设:网络凝聚。 \(J_{\text{social}} = -\beta_s \rho(W), \quad \beta_s > 0\)
有效财富: \(W'(W) = W - \beta_s N P(W)\)
自洽方程: \(P(W) = A \cdot e^{-(W - \beta_s N P(W))/\Theta} \Rightarrow P(W) e^{-\frac{\beta_s N}{\Theta} P(W)} = A e^{-W/\Theta}\)
令 $k’ = \frac{\beta_s N}{\Theta} > 0$,左边为 $h(P) = P e^{-k’P}$。
- 非单调性:$h(P)$ 在 $P = 1/k’$ 处取得最大值 $h_{\text{max}} = \frac{1}{k’} e^{-1}$
- 临界条件:当 $\Theta$ 过低(经济固化),$k’$ 很大,$h_{\text{max}}$ 很小,导致对某些 $W$ 无解。
相变与凝聚:
当 $\Theta < \Theta_c$,连续分布无法容纳全部人口,部分个体凝聚到单一财富点: \(P_{\text{total}}(W) = P_{\text{normal}}(W) + \frac{N_{\text{condensate}}}{N} \cdot \delta(W - W_{\text{condensate}})\)
社会学解释:顶层通过资本、信息和网络优势自我强化,形成赢家通吃局面。
第三部分:综合模型
现实财富分布是两类相互作用的混合:
- 中下层(费米子区):资源竞争激烈,分布被抑制,呈平坦化指数形态。
- 顶层(玻色子区):网络与资本正反馈,形成幂律尾(fat tail),远慢于指数衰减。
整体分布可近似为: \(P(W) \sim \begin{cases} \text{类指数} & \text{for } W \ll W^* \\ \text{幂律 } W^{-(1+\gamma)} & \text{for } W \gg W^* \end{cases}\)
这解释了“99% vs 1%”的二元结构。
附录
Beatrice魔法的物理依据是什么
神学假设
全知全能的神不存在(而计划经济的假设是神存在,可以用现有的运筹学工具白盒静态优化社会资源配置)。神不存在这一假设参考米塞斯《人的行动》和哈耶克三角《价格与生产》,大致是:
- 复杂系统的不可预测性
- 社会发展的创新需求(创新的需求来自于达尔文生存压力,例如百年耻辱)
- 消费偏好的主观性(例如代际改变)
因此Beatrice魔法类似于多智能体的强化学习,比运筹学规划更适合黑盒动态环境的优化。
不同主体在不同专业领域有不同的分工、认知、能力优势,作为神的眼睛和分身,所持有的认知碎片共同完成对于世界的拼图,在这个意义上,神是人类组织出来的共同体。
拼图机制(共识)
人类的组织需要一套共识机制完成,其核心和远古的图腾别无二样:通过符号完成自我与他者的混淆
现代社会根据具体功能划分成更为细致的符号系统:
语言、意识形态、民族、法律、主权货币、道德、文化、行为纲领、社会角色、企业商业计划书、家庭 …
不同共识符号具有不同的迭代周期和生命周期,参考热力学系统中不同粒子间的化学势
TBD
金融工具
杠杆:现有资源的分时复用(类似单个CPU可以被多个进程按时间片切分复用), 在私有制的基础上发展出的资源公有借用
得以存在的假设:
- 部分个体(央行——Beatrice代理人)现有资源储备充足(农业社会的原始积累)
- 需求的异质性,不同生产和商业活动所需的物理时间周期的差异(机器织毛衣只需数天,创造一个游戏需要数年,知识的研发生产和商业化盈利可能要几十上百年)
- 资源的异质性,不同主体能力异质性 (A的资源在B手里会发挥更大的作用)
催化剂
活化能
过渡态
作为原则的永恒?
利率时间偏好,其心理学的稳定性
个体稳定性:
1
2
3
4
5
6
7
8
9
10
11
选自《风险,人性与未来的前景》——Alan Greenspan:
在 1972年和 1990年开展了一项知名实验,
结果表明:4~6岁的儿童放弃即期享受的自制力,
会在多年之后表现在较高的中学会考成绩上,
能够推迟享受的儿童比控制力较差的儿童更容易获得成功。
2011年对同一批测试对象的跟踪研究再次证明了这个现象,
这表明人们的时间偏好水平保持着终身的稳定水平,
当然每个人的水平各不相同。
愿意为将来的更大回报而放弃即期享受的人,智力水平通常也更高。
代际稳定性:
1
2
3
4
5
6
7
8
9
10
11
选自《风险,人性与未来的前景》——Alan Greenspan:
时间偏好在代与代之间保持的稳定性有据可依,
早在公元前5世纪的希腊,利率水平的表现就已
非常接近于我们今天的市场。
英格兰银行在1694~1972年执行的官方政策利率
一直在2%~10%波动,在20世纪70年代后期的高
通货膨胀中提升到17%,此后又回到个位数的
历史区间。我们有充分的理由推断,
时间偏好没有明显的长期变动趋势。
魔法完成了什么?
资源在不同时空层面的(合理?)分配:
- 将资源能够分配到最能发挥其效用的地方(空间层面利差烫平)
- 将未来的收益转移到当下(时间层面利差烫平)
- 保险功能:通过共同体,降低个体的风险(参考热力学的根号n定律)
这样的合作机制使得达尔文演化的单位从个体过渡到更有效率的组织(超越基因的符号系统构建的文化种族),且被全球化的历史证实可以scalable到几十亿的合作规模
不合理的地方就是个体的盈利机会(包括科技突破、金融套利、新需求发现、新危机造成的均衡shift等多种活动)
重要的历史经验
1930~ 胡佛 罗斯福时代
金字塔收缩到T1时,为了避免通缩,即为了保持T1~Tn的绝对宽度不变,需要扩充T0的绝对宽度以保持金字塔的相对形状稳定。在T0数量有限的情况下,黄金迎来re-valuation(可以是法币挤兑,也可以是官方强制重新定价并锁死流动性)
市场信号:美债(尤其是长债)遭到大量抛售,长债的收益率增长快于短债
金价在1920~1932稳定在$20/oz~$21/oz
罗斯福的操作:
- 1933年4月,行政命令6102要求美国人将黄金硬币、黄金条块和黄金证书在1933年5月1日前交给联邦储备银行,以市场价$20.67/oz兑换。
- 1934年1月,国会立法颁布《黄金储备法案》将黄金价格强制定为$35/oz,并禁止私人兑换黄金 (这一新价格仅适用于政府之间的交易,普通公民在1933年交出黄金时,仍按照每盎司20.67美元的价格进行兑换)
- 允许财政部在国际上购买黄金,以使美元在外汇市场上进一步贬值
伦敦黄金市场在1931-1939年间为自由市场,金价受供需影响,私人囤积黄金显著。
美国直到1974年放松黄金禁令(1975年1月1日生效),允许个人投资者拥有黄金。
里根大循环
TBD
2000年互联网泡沫
1
2
3
4
5
6
选自《风险,人性与未来的前景》——Alan Greenspan:
某些学者倾向于通过逐步收紧货币政策,以渐进方式去除泡沫,
但在实际操作中此类渐进政策似乎从来没有奏效过。
今天看来,美联储在1994年面临尚未成形的互联网泡沫
时采用的逐步收紧货币的做法,就可能起到了适得其反的效果。
此次危机被美联储提前注意到,收紧了货币政策,仍然避免不了危机。
个人猜测原因: 央行只能控制金字塔顶端,底层的资源配置仍然由分布式的主体决定,危机的根源在于从众效应导致的资源错配和预期违约。
2008年金融危机
TBD
危机中的黄金
黄金在危机前和危机后一般都会有大的升值 ,但在危机年份买卖双方力量都很强。 例如2008年黄金价格几乎没变,波动率极高。
原因:
- 大量机构和散户爆仓,不得不抛售黄金去支付所需的保证金
- 美元流动性暂时收紧
石油
super contango机会
2020年 仓储能力
地缘冲突期间
铜金比价
某种危机指标?
日本30年 人口结构变化
日本房地产于1991崩盘,此时财政债务占GDP的比重为63% (还是比较低的,目前已超过250%)
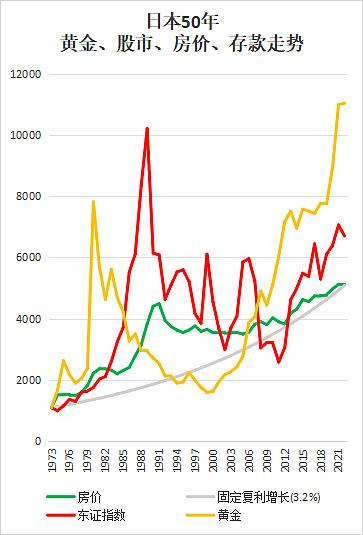
图:日元计价资产
T0黄金每次都稳定吸收了流动性(量化宽松造成了T2日元贬值,T0黄金和T1美元都是相对于其的外汇)
房价迅速下跌后缓慢下跌数十年,最终在2012年和年化3.2%的固收终点重合,说明日本人花了20年还完了房贷
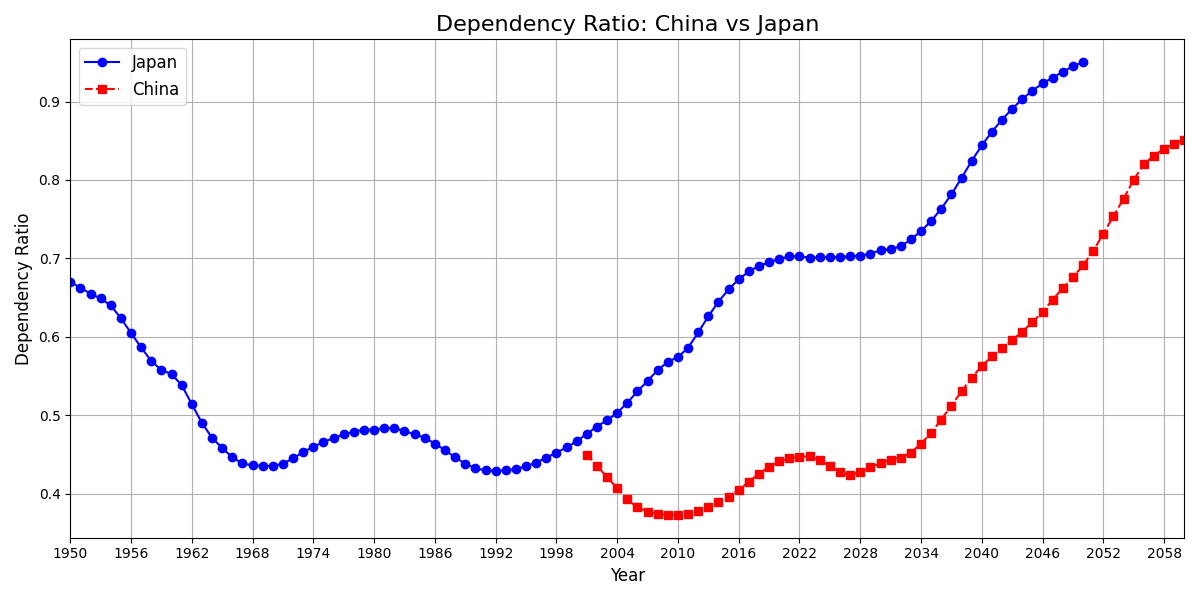
大约在2000年(泡沫破裂十年后)日本才逐渐迈入老龄化和少子化,人口抚养比逐步上升,直到2018年抚养比接近70%, 此时二战后婴儿潮的老年人口年龄较高(2025-1947=78岁),因自然凋亡将迅速减少,完成财富的代际传承。(日本男性的平均寿命81岁,女性87岁)
根据预测数据,2018~2032期间日本抚养比(根据其余人口/劳动年龄人口计算)几乎保持不变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
# https://population-pyramid.net/zh-cn/pp/%E6%97%A5%E6%9C%AC
# https://population-pyramid.net/zh-cn/pp/%E4%B8%AD%E5%9B%BD
# 劳动年龄人口占比
jp_data = ["59.88%", "60.15%", "60.43%", "60.65%", "60.98%", "61.59%", "62.32%", "63.04%", "63.74%", "64.20%", "64.42%", "65.01%", "66.05%", "67.11%", "67.98%", "68.58%", "69.15%", "69.52%", "69.64%", "69.68%", "69.68%", "69.54%", "69.21%", "68.83%", "68.51%", "68.23%", "67.99%", "67.78%", "67.61%", "67.50%", "67.50%", "67.41%", "67.40%", "67.60%", "67.76%", "67.98%", "68.32%", "68.72%", "69.15%", "69.54%", "69.82%", "69.96%", "69.98%", "69.96%", "69.86%", "69.70%", "69.47%", "69.17%", "68.87%", "68.55%", "68.18%", "67.75%", "67.32%", "66.96%", "66.54%", "65.97%", "65.35%", "64.78%", "64.21%", "63.78%", "63.53%", "63.06%", "62.29%", "61.50%", "60.80%", "60.23%", "59.76%", "59.41%", "59.16%", "59.00%", "58.86%", "58.73%", "58.74%", "58.79%", "58.78%", "58.77%", "58.76%", "58.74%", "58.70%", "58.62%", "58.47%", "58.42%", "58.30%", "58.00%", "57.65%", "57.22%", "56.71%", "56.13%", "55.48%", "54.82%", "54.23%", "53.72%", "53.28%", "52.89%", "52.54%", "52.25%", "52.00%", "51.80%", "51.60%", "51.42%", "51.27%"]
cn_data = ["68.98%", "69.67%", "70.38%", "71.08%", "71.82%", "72.35%", "72.62%", "72.78%", "72.86%", "72.86%", "72.80%", "72.61%", "72.34%", "72.01%", "71.63%", "71.20%", "70.67%", "70.16%", "69.74%", "69.40%", "69.21%", "69.10%", "69.09%", "69.33%", "69.68%", "70.07%", "70.26%", "70.06%", "69.76%", "69.52%", "69.29%", "69.16%", "68.86%", "68.33%", "67.69%", "66.92%", "66.13%", "65.35%", "64.61%", "64.01%", "63.49%", "63.06%", "62.67%", "62.25%", "61.79%", "61.29%", "60.71%", "60.17%", "59.68%", "59.14%", "58.50%", "57.76%", "57.02%", "56.31%", "55.55%", "54.95%", "54.61%", "54.36%", "54.17%", "54.01%"]
# 数据预处理:去掉百分号并转换为浮点数,然后计算抚养比
def calculate_dependency_ratio(data):
return [(100 - float(value.strip("%"))) / float(value.strip("%")) for value in data]
jp_dependency_ratio = calculate_dependency_ratio(jp_data)
cn_dependency_ratio = calculate_dependency_ratio(cn_data)
# 定义年份范围
jp_years = list(range(1950, 1950 + len(jp_data))) # 日本年份从 1950 到 2050
cn_years = list(range(2001, 2001 + len(cn_data))) # 中国年份从 2001 到 2060
plt.figure(figsize=(12, 6)) # 设置图像大小
plt.plot(jp_years, jp_dependency_ratio, marker="o", linestyle="-", color="b", label="Japan") # 日本数据
plt.plot(cn_years, cn_dependency_ratio, marker="s", linestyle="--", color="r", label="China") # 中国数据
# 添加标题和标签
plt.title("Dependency Ratio: China vs Japan", fontsize=16)
plt.xlabel("Year", fontsize=12)
plt.ylabel("Dependency Ratio", fontsize=12)
plt.legend(loc="upper left", fontsize=12) # 添加图例
plt.grid(True)
# 设置 x 轴刻度
min_year = min(jp_years[0], cn_years[0]) # 最小年份
max_year = max(jp_years[-1], cn_years[-1]) # 最大年份
plt.xlim(min_year, max_year) # 设置 x 轴范围
plt.gca().xaxis.set_major_locator(MaxNLocator(nbins=20)) # 自动调整刻度数量
# 保存图像
plt.tight_layout()
plt.savefig("cn_jp_dependency_ratio.png")
可以看到,安倍晋三在2012年这次量化宽松后日本股市稳定在高位
投资为什么失败
预测市场的未来走势是错误的做法
1
2
3
4
5
选自《风险,人性与未来的前景》——Alan Greenspan:
我们很难判断雪面上的小块裂缝是否会触发大规模雪崩,
由于同样的原因,也很难预先判断何种事件将触发大规
模金融危机,尤其是2008年9月那种量级的危机。
大多数基金经理无法跑赢指数
TBD
黑天鹅
身体每天都会有细胞癌变
TBD
辩论赛和马后炮式的由果溯因
每天都能找出来上百个利好和利空的新闻
TBD
Erica和Dlanor的解答
Erica
没有爱,便看不到?
正因为有了爱,所以才看到了不存在的东西
Dlanor
有关魔女的处刑,怜悯、无用的修饰
TBD
TBD
应该怎么做
遵循Robustness原则
即使明天是诸神之战和大洪水
diversity实际是在做什么
VC届为什么不允许该行业更有专业知识的研究员直接参与投资
TBD
均衡过程: 交换
正确的估值
交易的是利差
TBD
金藏的解答
胜利 魔法 出色
TBD
闪电与雷鸣
同一事件的不同测量,在不同空间有不同传播速度
TBD