EM算法

发表于 2025/12/04 更新于 2025/12/04

作者 gctoph

32 分钟阅读

EM算法

参考:

《Deep Learning : Foundations and Concepts》by Christopher Bishop and Hugh Bishop

K-means算法

K-means 硬分配

K-means 的目标是将数据集 $X = {x_1, …, x_N}$ 分成 $K$ 类。可以看作优化以下目标函数：

\[J = \sum_{n=1}^N \sum_{k=1}^K r_{nk} ||x_n - \mu_k||^2\]

其中 $r_{nk} \in {0, 1}$ 是指示变量（样本 $n$ 是否属于簇 $k$），$\mu_k$ 是簇中心。

K-means 的迭代过程：

固定 $\mu_k$，优化 $r_{nk}$：把每个点分配给最近的中心（E步）。
固定 $r_{nk}$，优化 $\mu_k$：重新计算中心为簇内点的均值（M步）。

K-means 的局限与 soft 思想

K-means 有两个设定：

硬分配：一个点要么属于 A，要么属于 B，不能“70%属于A，30%属于B”。
球形簇：它假设所有簇的方差相同且是球形的。

如果将 $r_{nk}$ 放宽到 $[0, 1]$ 区间，表示概率，得到 soft K-means。如果进一步允许每个簇有自己的形状（协方差矩阵 $\Sigma_k$）和大小（混合系数 $\pi_k$），就得到 混合高斯模型 (GMM)。

EM算法

EM (Expectation-Maximization) 算法是用于含有隐变量 (Latent Variables) 的概率模型参数估计的通用方法。

问题定义

观测数据：$X$
隐变量：$Z$
参数：$\theta$
目标：最大化观测数据的对数似然函数 (Log-Likelihood)：
\[\ln p(X|\theta) = \ln \left( \sum_Z p(X, Z | \theta) \right)\]

但由于 求和在对数内部，该函数通常无法直接求导优化，因为：

无法将 $\sum_Z$ 从 $\ln(\cdot)$ 中提出；
对 $\theta$ 求导后得不到解析解。

在大多数含隐变量的模型中（如高斯混合模型），联合分布 $p(X, Z \mid \theta)$ 的形式是明确给定的

例如，在高斯混合模型中：
\[p(X, Z \mid \theta) = \prod_{n=1}^N \prod_{k=1}^K \left[ \pi_k \, \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \right]^{z_{nk}}\]
其中 $ z_{nk} = 1 $ 表示第 $ n $ 个样本属于第 $ k $ 个高斯成分。 $\theta$ 代表需要估计的 $\pi_k$, $\mu_k$, $\Sigma_k$.
关键点：$ p(X, Z \mid \theta) $ 通常易于写出、易于求导。

变分下界 (ELBO)

我们可以引入关于隐变量 $Z$ 的任意分布 $q(Z)$。

从恒等式出发：

\[\ln p(X \mid \theta) = \sum_Z q(Z) \ln p(X \mid \theta)\]

利用贝叶斯定理 $p(X, Z \mid \theta) = p(X \mid \theta) p(Z \mid X, \theta)$，可得：

\[\ln p(X \mid \theta) = \sum_Z q(Z) \ln \left( \frac{p(X, Z \mid \theta)}{p(Z \mid X, \theta)} \right)\]

将分子分母同时除以 $q(Z)$，再拆分对数：

\[\begin{aligned} \ln p(X \mid \theta) &= \sum_Z q(Z) \ln \left( \frac{p(X, Z \mid \theta)}{q(Z)} \cdot \frac{q(Z)}{p(Z \mid X, \theta)} \right) \\ &= \underbrace{ \sum_Z q(Z) \ln \frac{p(X, Z \mid \theta)}{q(Z)} }_{\mathcal{L}(q, \theta)} + \underbrace{ \sum_Z q(Z) \ln \frac{q(Z)}{p(Z \mid X, \theta)} }_{KL(q \,\|\, p(Z \mid X, \theta))} \end{aligned}\]

即得到核心分解式：

\[\boxed{ \ln p(X \mid \theta) = \mathcal{L}(q, \theta) + KL\big( q(Z) \,\|\, p(Z \mid X, \theta) \big) }\]

其中：

$\mathcal{L}(q, \theta)$ 称为 证据下界（Evidence Lower Bound, ELBO）
$KL(\cdot \,|\, \cdot) \ge 0$ 是 KL 散度，当且仅当 $q(Z) = p(Z \mid X, \theta)$ 时取等号（即 $KL = 0$）

\[\mathcal{L}(q, \theta) = \sum_Z q(Z) \ln p(X, Z \mid \theta) - \sum_Z q(Z) \ln q(Z)\]

第一项：联合对数似然在 $q$ 下的期望
第二项：$q(Z)$ 的熵

EM 算法流程

对任意固定的 $\theta$，$\ln p(X \mid \theta)$ 是一个与 $q$ 无关的常数。

由于左边为常数，最大化 $\mathcal{L}(q, \theta)$ 等价于最小化 KL 散度, 而当且仅当 $q(Z) = p(Z \mid X, \theta)$ 时，$KL = 0$

因此最大化对数似然的问题变成了最大化ELBO的问题。

交替优化 $q$ 和 $\theta$

E 步（Expectation Step）

固定当前参数 $\theta^{\text{old}}$
选择 $q(Z)$ 使得 ELBO 最大（即 KL 最小）
由 KL 非负性，最优解为：

\[q(Z) = p(Z \mid X, \theta^{\text{old}})\]

此时 $KL = 0$，ELBO 等于当前对数似然：

\[\ln p(X \mid \theta^{\text{old}}) = \mathcal{L}(q, \theta^{\text{old}}) = Q(\theta, \theta^{\text{old}}) + \text{const}\]

其中：

\[Q(\theta, \theta^{\text{old}}) = \mathbb{E}_{Z \sim p(Z \mid X, \theta^{\text{old}})} \left[ \ln p(X, Z \mid \theta) \right] = \sum_Z p(Z \mid X, \theta^{\text{old}}) \ln p(X, Z \mid \theta)\]

而const是q的熵

M 步（Maximization Step）

固定 $q(Z) = p(Z \mid X, \theta^{\text{old}})$
最大化 ELBO 关于 $\theta$：

\[\theta^{\text{new}} = \arg\max_\theta \mathcal{L}(q, \theta^{\text{old}}) = \arg\max_\theta Q(\theta, \theta^{\text{old}})\]

步骤	目标	操作
E 步	用当前参数计算隐变量后验	$q(Z) = p(Z \mid X, \theta^{\text{old}})$
M 步	用“软标签”更新参数	$\theta^{\text{new}} = \arg\max_\theta \mathbb{E}_{q(Z)}[\ln p(X, Z \mid \theta)]$

收敛性：单调有界

每次 E 步后：$\mathcal{L}(q, \theta^{\text{old}}) = \ln p(X \mid \theta^{\text{old}})$
每次 M 步后：$\mathcal{L}(q, \theta^{\text{new}}) \ge \mathcal{L}(q, \theta^{\text{old}})$
而 $\ln p(X \mid \theta^{\text{new}}) \ge \mathcal{L}(q, \theta^{\text{new}})$

因此：

\[\ln p(X \mid \theta^{\text{new}}) \ge \ln p(X \mid \theta^{\text{old}})\]

即 对数似然单调递增。若似然函数有上界（通常成立），则 EM 算法收敛到局部极大值或鞍点。

混合高斯模型

K-means 虽然简单高效，但存在两个主要的局限性：

硬分配：它强制每个样本 $100\%$ 属于某一个簇，无法描述处于边界的不确定性。
球形假设：K-means 假设簇是球形的且方差相等。如果数据分布是椭圆形的（变量间存在相关性）或者簇的大小不一，K-means 的效果会很差。

混合高斯模型 (Gaussian Mixture Model, GMM) 通过以下方式解决这些问题：

概率组合：假设数据是由 $K$ 个高斯分布（成分）线性组合生成的。
软分配：计算样本属于每个高斯成分的后验概率。
灵活形状：每个成分有自己的均值 $\mu_k$ 和协方差矩阵 $\Sigma_k$。

模型定义

假设数据由 $K$ 个高斯分布混合生成：

\[p(x) = \sum_{k=1}^K \pi_k \mathcal{N}(x \mid \mu_k, \Sigma_k)\]

其中：

$\pi_k$ 是 混合系数 (Mixing Coefficient)，满足 $0 \le \pi_k \le 1$ 且 $\sum_{k=1}^K \pi_k = 1$。
可以理解为选择第 $k$ 个簇的先验概率 $p(z_k=1) = \pi_k$。

隐变量 $z_{nk}\in {0, 1}$，表示第 $n$ 个样本是否属于第 $k$ 类。

先验： $p(z_n) = \prod_{k=1}^K \pi_k^{z_{nk}}$
条件概率： $p(x_n | z_n) = \prod_{k=1}^K \mathcal{N}(x_n | \mu_k, \Sigma_k)^{z_{nk}}$

完全数据对数似然：

\[\ln p(X, Z | \mu, \Sigma, \pi) = \sum_{n=1}^N \sum_{k=1}^K z_{nk} \{ \ln \pi_k + \ln \mathcal{N}(x_n | \mu_k, \Sigma_k) \}\]

E 步：计算责任度 (Responsibilities)

我们需要计算隐变量的后验概率 $p(Z|X, \theta^{old})$ , 即第 $n$ 个点属于第 $k$ 个簇的概率，记为 $\gamma_{nk}$：

\[\gamma_{nk} = p(z_{nk}=1 | x_n) = \frac{\pi_k \mathcal{N}(x_n | \mu_k, \Sigma_k)}{\sum_{j=1}^K \pi_j \mathcal{N}(x_n | \mu_j, \Sigma_j)}\]

可以看作是 K-means 中 $r_{nk}$ 的“软化”版本。$\gamma(z_{nk}) \in [0, 1]$，表示第 $k$ 个簇对解释第 $n$ 个样本点有多大的“责任”。

M 步：参数更新

最大化 $Q$ 函数：

\[Q = \sum_{n=1}^N \sum_{k=1}^K \gamma_{nk} \{ \ln \pi_k + \ln \mathcal{N}(x_n | \mu_k, \Sigma_k) \}\] \[Q \propto \sum_{n=1}^N \sum_{k=1}^K \gamma_{nk} \left( \ln \pi_k - \frac{1}{2}\ln|\Sigma_k| - \frac{1}{2}(x_n - \mu_k)^T \Sigma_k^{-1} (x_n - \mu_k) \right)\]

定义有效样本数 $N_k = \sum_{n=1}^N \gamma_{nk}$ 。

更新均值 $\mu_k$

相关项：

\[J(\mu_k) = \sum_{n=1}^N \gamma_{nk} \left( - \frac{1}{2}(x_n - \mu_k)^T \Sigma_k^{-1} (x_n - \mu_k) \right)\]

推导：

$\frac{\partial Q}{\partial \mu_k} = \sum_{n=1}^N \gamma_{nk} \left( -\frac{1}{2} \cdot (-2) \Sigma_k^{-1} (x_n - \mu_k) \right)$ $= \Sigma_k^{-1} \sum_{n=1}^N \gamma_{nk} (x_n - \mu_k) = 0$

由于 $\Sigma_k^{-1}$ 是正定矩阵（可逆），我们可以两边同乘 $\Sigma_k$ 将其消除：

\[\sum_{n=1}^N \gamma_{nk} x_n - \sum_{n=1}^N \gamma_{nk} \mu_k = 0\] \[\sum_{n=1}^N \gamma_{nk} x_n = \mu_k \sum_{n=1}^N \gamma_{nk} = \mu_k N_k\]

结果： $\boxed{ \mu_k^{new} = \frac{1}{N_k} \sum_{n=1}^N \gamma_{nk} x_n }$

更新协方差 $\Sigma_k$

相关项： $J(\Sigma_k) = \sum_{n=1}^N \gamma_{nk} \left( - \frac{1}{2}\ln|\Sigma_k| - \frac{1}{2}(x_n - \mu_k)^T \Sigma_k^{-1} (x_n - \mu_k) \right)$

这里使用迹 (Trace) 技巧来简化二次型的求导。因为标量的迹等于其自身： $(x-\mu)^T \Sigma^{-1} (x-\mu) = \text{Tr}\left( (x-\mu)^T \Sigma^{-1} (x-\mu) \right) = \text{Tr}\left( \Sigma^{-1} (x-\mu)(x-\mu)^T \right)$。

求导工具（矩阵微积分）：

$\frac{\partial \ln |A|}{\partial A} = A^{-T} = A^{-1}$ (若 $A$ 对称)
$\frac{\partial \text{Tr}(A^{-1}B)}{\partial A} = -A^{-1} B A^{-1}$

推导： $\frac{\partial Q}{\partial \Sigma_k} = \sum_{n=1}^N \gamma_{nk} \left( -\frac{1}{2} \Sigma_k^{-1} - \frac{1}{2} \frac{\partial}{\partial \Sigma_k} \text{Tr}\left( \Sigma_k^{-1} (x_n - \mu_k)(x_n - \mu_k)^T \right) \right)$

利用工具 2： $= \sum_{n=1}^N \gamma_{nk} \left( -\frac{1}{2} \Sigma_k^{-1} - \frac{1}{2} \left[ - \Sigma_k^{-1} (x_n - \mu_k)(x_n - \mu_k)^T \Sigma_k^{-1} \right] \right)$

令导数为 0，并去掉系数 $-\frac{1}{2}$： $\sum_{n=1}^N \gamma_{nk} \Sigma_k^{-1} = \sum_{n=1}^N \gamma_{nk} \Sigma_k^{-1} (x_n - \mu_k)(x_n - \mu_k)^T \Sigma_k^{-1}$

为了解出 $\Sigma_k$，在等式左边乘 $\Sigma_k$，右边乘 $\Sigma_k$： $\Sigma_k \left( \sum_{n=1}^N \gamma_{nk} \Sigma_k^{-1} \right) \Sigma_k = \Sigma_k \left( \sum_{n=1}^N \gamma_{nk} \Sigma_k^{-1} (x_n - \mu_k)(x_n - \mu_k)^T \Sigma_k^{-1} \right) \Sigma_k$

化简（ $\Sigma \Sigma^{-1} = I$）： $\sum_{n=1}^N \gamma_{nk} \Sigma_k = \sum_{n=1}^N \gamma_{nk} (x_n - \mu_k)(x_n - \mu_k)^T$

\[N_k \Sigma_k = \sum_{n=1}^N \gamma_{nk} (x_n - \mu_k)(x_n - \mu_k)^T\]

结果： $\boxed{ \Sigma_k^{new} = \frac{1}{N_k} \sum_{n=1}^N \gamma_{nk} (x_n - \mu_k^{new})(x_n - \mu_k^{new})^T }$

更新混合系数 $\pi_k$

约束条件：不能直接求导，因为 $\pi_k$ 必须满足约束 $\sum_{k=1}^K \pi_k = 1$。需要使用 拉格朗日乘子法 (Lagrange Multipliers)。

构造拉格朗日函数：只保留含 $\pi_k$ 的项，并加入约束： $L(\pi, \lambda) = \sum_{n=1}^N \sum_{k=1}^K \gamma_{nk} \ln \pi_k + \lambda \left( \sum_{k=1}^K \pi_k - 1 \right)$

求导： $\frac{\partial L}{\partial \pi_k} = \sum_{n=1}^N \gamma_{nk} \frac{1}{\pi_k} + \lambda = 0$

移项整理： $N_k = - \lambda \pi_k$ 或者写作： $\pi_k = \frac{N_k}{-\lambda}$

求解 $\lambda$：对所有 $k$ 求和（利用 $\sum \pi_k = 1$）： $\lambda = -N$

结果： $\boxed{ \pi_k^{new} = \frac{N_k}{N} }$

用 EM 框架重写 K-means

K-means 实际上是 高斯混合模型 (GMM) 在特定极限条件下的特例。通过引入一个参数 $\epsilon$（方差）并令其趋于 0，来严格导出 K-means 算法。

模型设定

假设数据由 $K$ 个高斯分布生成，约束：

协方差矩阵固定且相同：$\Sigma_k = \epsilon I$（球形，且方差为 $\epsilon$）。
混合系数相同：$\pi_k = \frac{1}{K}$（每个簇的先验概率相等）。

此时，给定隐变量 $z_{nk}=1$（样本 $n$ 属于簇 $k$），观测数据的条件概率为： $p(x_n \mid z_{nk}=1, \mu_k) = \frac{1}{(2\pi\epsilon)^{D/2}} \exp \left( -\frac{1}{2\epsilon} ||x_n - \mu_k||^2 \right)$

需要估计的参数仅为中心 $\theta = { \mu_1, …, \mu_K }$。

E 步

根据 EM 框架，E 步需要计算隐变量的后验分布 $q(Z) = p(Z \mid X, \theta^{\text{old}})$。对于第 $n$ 个样本属于第 $k$ 个簇的概率 $r_{nk}$（即责任度 responsibility）：

\[r_{nk} = p(z_{nk}=1 \mid x_n, \theta) = \frac{\pi_k p(x_n \mid \mu_k, \epsilon)}{\sum_{j=1}^K \pi_j p(x_n \mid \mu_j, \epsilon)}\]

代入高斯分布公式并消去常数项（$\pi_k$ 和归一化因子）：

\[r_{nk} = \frac{\exp \left( -\frac{1}{2\epsilon} ||x_n - \mu_k||^2 \right)}{\sum_{j=1}^K \exp \left( -\frac{1}{2\epsilon} ||x_n - \mu_j||^2 \right)}\]

当 $\epsilon \to 0$ 时，上式中的指数项会被最小的距离 $||x_n - \mu_k||^2$ 主导。

如果 $k = \arg\min_j ||x_n - \mu_j||^2$ （即 $\mu_k$ 是最近的中心），则 $r_{nk} \to 1$。
否则，$r_{nk} \to 0$。

这正是 K-means 的 硬分配 (Hard Assignment) 步骤： $r_{nk} = \begin{cases} 1 & \text{if } k = \arg\min_j ||x_n - \mu_j||^2 \\ 0 & \text{otherwise} \end{cases}$

M 步

忽略与 $\mu_k$ 无关的常数项，最大化 $Q$ 等价于最小化以下目标函数：

\[J = \sum_{n=1}^N r_{nk} ||x_n - \mu_k||^2\]

这正是 K-means 的 失真函数 (Distortion Measure)。对 $\mu_k$ 求导并令其为 0，得到：

\[\mu_k = \frac{\sum_{n=1}^N r_{nk} x_n}{\sum_{n=1}^N r_{nk}}\]

这正是 K-means 的 中心更新 步骤。

GMM 代码

  
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse

# 设置随机种子
np.random.seed(42)

# ==========================================
# 混合高斯模型 (GMM) - EM 算法实现
# ==========================================

class GMM_EM:
    def __init__(self, K, max_iter=100, tol=1e-4):
        self.K = K
        self.max_iter = max_iter
        self.tol = tol
        
    def fit(self, X):
        N, D = X.shape
        # 初始化
        idx = np.random.choice(N, self.K, replace=False)
        self.mu = X[idx]
        self.sigma = [np.eye(D) for _ in range(self.K)]
        self.pi = np.ones(self.K) / self.K
        
        log_likelihoods = []
        
        for i in range(self.max_iter):
            # --- E-Step ---
            responsibility = np.zeros((N, self.K))
            for k in range(self.K):
                responsibility[:, k] = self.pi[k] * self._multivariate_gaussian(X, self.mu[k], self.sigma[k])
            
            total_prob = np.sum(responsibility, axis=1, keepdims=True)
            responsibility = responsibility / (total_prob + 1e-10)  # 避免除零
            
            log_likelihoods.append(np.sum(np.log(total_prob + 1e-10)))
            
            # --- M-Step ---
            Nk = np.sum(responsibility, axis=0) + 1e-10  # 防止除零
            
            for k in range(self.K):
                self.mu[k] = (responsibility[:, k] @ X) / Nk[k]
                
                diff = X - self.mu[k]
                weighted_cov = (responsibility[:, k][:, None] * diff).T @ diff
                self.sigma[k] = weighted_cov / Nk[k] + 1e-6 * np.eye(D) # + 1e-6 * np.eye(D) 添加小的正则项，防止协方差矩阵奇异（不可逆）。
                
                self.pi[k] = Nk[k] / N
            
            # 检查收敛
            if i > 0 and abs(log_likelihoods[-1] - log_likelihoods[-2]) < self.tol:
                break
        
        # 保存最后的 responsibility 用于可视化
        self.responsibility = responsibility
        return log_likelihoods

    def _multivariate_gaussian(self, X, mu, sigma):
        D = X.shape[1]
        det = np.linalg.det(sigma)
        inv = np.linalg.inv(sigma)
        norm_const = 1.0 / (np.power(2 * np.pi, D / 2) * np.sqrt(det + 1e-10))
        diff = X - mu
        exponent = -0.5 * np.einsum('ij,ji->i', diff @ inv, diff.T)
        return norm_const * np.exp(exponent)

# ==========================================
# 生成数据
# ==========================================

true_mu = [[-2, -2], [2, 2], [-2, 2]]
true_sigma = [
    [[1, 0.75], [0.75, 1]],
    [[1, -0.75], [-0.75, 1]],
    [[2, 0], [0, 2]]
]
X_gmm = []
for m, s in zip(true_mu, true_sigma):
    X_gmm.append(np.random.multivariate_normal(m, s, 150))
X_gmm = np.vstack(X_gmm)

# ==========================================
# 训练 GMM
# ==========================================
gmm = GMM_EM(K=3)
log_likelihoods_gmm = gmm.fit(X_gmm)

# ==========================================
# 可视化：根据后验概率加权 RGB 着色
# ==========================================

# 定义三种基色：簇0=R, 簇1=G, 簇2=B
base_colors = np.array([
    [1, 0, 0],   # Red
    [0, 1, 0],   # Green
    [0, 0, 1]    # Blue
])

# gamma 是 (N, 3)，每行是该点属于三个簇的后验概率
# 加权混合：X @ base_colors 得到每个点的 RGB 颜色
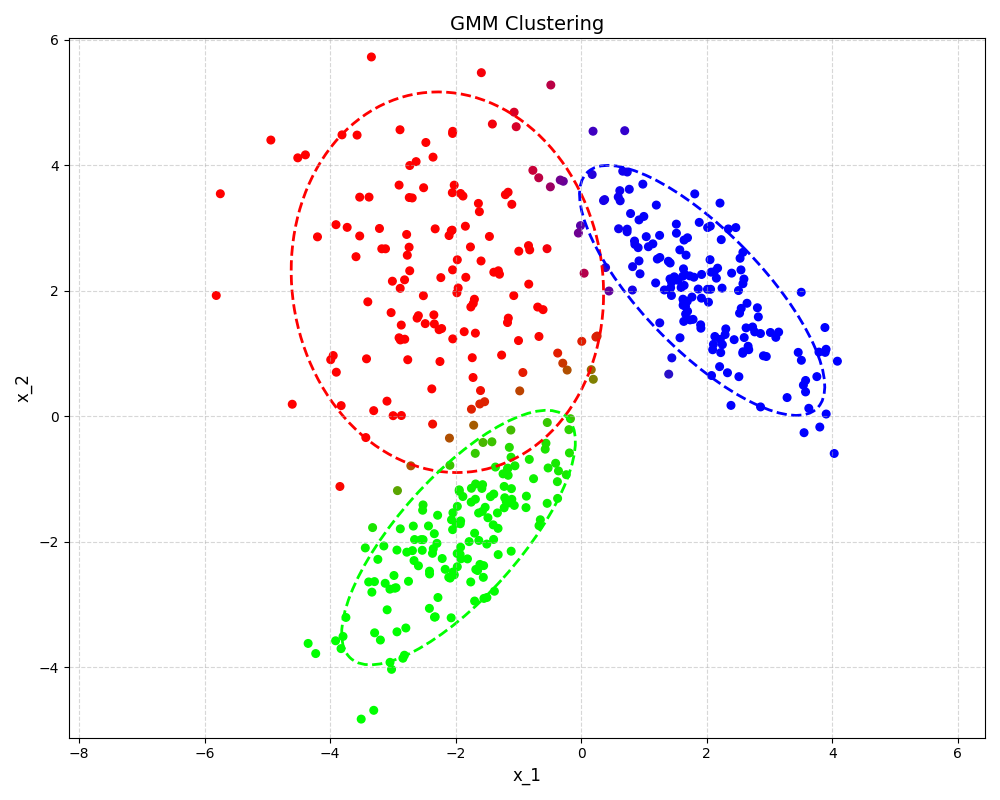
colors = gmm.responsibility @ base_colors  # shape: (N, 3)

# 绘图
plt.figure(figsize=(10, 8))
plt.scatter(X_gmm[:, 0], X_gmm[:, 1], c=colors, alpha=1, s=30)

# 绘制高斯椭圆
for k in range(3):
    
    # 协方差椭圆
    vals, vecs = np.linalg.eigh(gmm.sigma[k])
    order = vals.argsort()[::-1]
    vals, vecs = vals[order], vecs[:, order]
    theta = np.degrees(np.arctan2(*vecs[:, 0][::-1]))
    width, height = 2 * 2 * np.sqrt(vals)  # 2个标准差
    ell = Ellipse(xy=gmm.mu[k], width=width, height=height, angle=theta,
                  edgecolor=base_colors[k], lw=2, facecolor='none', linestyle='--')
    plt.gca().add_patch(ell)

plt.title("GMM Clustering", fontsize=14)
plt.xlabel("x_1", fontsize=12)
plt.ylabel("x_2", fontsize=12)
plt.axis('equal')
plt.grid(True, linestyle='--', alpha=0.5)
plt.tight_layout()
plt.show()

GMM 的协方差更新需要正则化（代码中加了 1e-6 * eye），否则当某个点独自成为一类时，方差趋于 0，似然趋于无穷大（奇点问题）。

VAE

生成建模

设观测数据集为 $X = {x_1, x_2, \ldots, x_N}$，其生成过程由以下两步构成：

从先验分布 $p(z)$ 中采样隐变量 $z$，通常假设 $z \sim \mathcal{N}(0, I)$；
给定隐变量 $z$，通过参数化的生成模型（解码器） $p(x|z; w)$ 生成观测数据 $x$，其中 $w$ 为模型参数。

目标是通过最大似然估计学习生成模型参数 $w$，即最大化对数似然函数：

\[\max_w \log p(X; w) = \sum_{n=1}^N \log p(x_n; w).\]

然而，边缘似然 $p(x; w)$ 的计算涉及对隐变量的积分： $p(x; w) = \int p(x|z; w) p(z) \, dz.$ 当隐变量维度较高且生成模型为非线性复杂函数（如神经网络）时，该积分不可解析计算，导致直接优化对数似然不可行。

变分推断与证据下界（ELBO）

引入一个近似分布 $q(z)$。可以对 $\ln p(x)$ 做如下分解：

\[\begin{aligned} \ln p(x) &= \int q(z) \ln p(x) dz \quad \text{(因为 $\int q(z)dz=1$, $\ln p(x)$ 与 $z$ 无关)} \\ &= \int q(z) \ln \frac{p(x, z)}{p(z|x)} dz \quad \text{(贝叶斯公式)} \\ &= \int q(z) \ln \left( \frac{p(x, z)}{q(z)} \cdot \frac{q(z)}{p(z|x)} \right) dz \quad \text{(上下同乘 $q(z)$)} \\ &= \underbrace{\int q(z) \ln \frac{p(x, z)}{q(z)} dz}_{\mathcal{L}(q, w) \text{: ELBO}} + \underbrace{\int q(z) \ln \frac{q(z)}{p(z|x)} dz}_{\text{KL}(q || p(z|x))} \end{aligned}\] \[\ln p(x) = \mathcal{L} + \text{KL}(q || p_{posterior})\]

我们不再直接优化 $\ln p(x)$，而是去最大化 ELBO ($\mathcal{L}$)。

摊销推断 (Amortized Inference)

在传统变分推断中，每个数据点 $x_n$ 需独立优化其对应的变分分布 $q_n(z)$，计算代价高昂。

摊销推断（Amortized Inference）通过引入一个共享的编码器网络 $q_\phi(z|x)$ 来实现参数共享：

\[q(z) \leftarrow q_\phi(z|x),\]

其中 $\phi$ 为编码器参数。该网络以 $x$ 为输入，输出隐变量 $z$ 的分布参数（如高斯分布的均值与方差）。

将联合分布 $p(x, z) = p(x|z; w)p(z)$ 代入 ELBO，可得具体形式：

\[\mathcal{L}(\phi, w) = \mathbb{E}_{q_\phi(z|x)}\big[ \log p(x|z; w) \big] - D_{\mathrm{KL}}\big( q_\phi(z|x) \,\|\, p(z) \big).\]

该目标函数包含两个关键组成部分：

重构项：鼓励模型在给定 $z$ 下能高概率地重建 $x$；
正则项：促使编码器输出的后验分布靠近先验分布 $p(z) = \mathcal{N}(0, I)$，防止过拟合并实现隐空间的结构化。

假设 $q_\phi(z|x) = \mathcal{N}(\mu, \text{diag}(\sigma^2))$

重参数化技巧 (The Reparameterization Trick)

为使用随机梯度下降（SGD）优化 $\mathcal{L}(\phi, w)$，需对期望项进行可微估计。

若直接采样：

\[z \sim \mathcal{N}(\mu_\phi(x), \sigma_\phi^2(x)),\]

则采样操作阻断了从损失函数到 $\phi$ 的梯度流。

重参数化技巧将随机性外置：

\[z = \mu_\phi(x) + \sigma_\phi(x) \odot \varepsilon, \quad \varepsilon \sim \mathcal{N}(0, I),\]

其中 $\odot$ 表示逐元素乘积。此时 $z$ 为 $\mu_\phi(x)$、$\sigma_\phi(x)$ 与独立噪声 $\varepsilon$ 的确定性函数，从而使得梯度可通过链式法则反向传播至编码器参数 $\phi$。

计算

KL 散度

前提条件：

先验分布 $p(z)$ 是标准正态分布：
\[p(z) = \mathcal{N}(0, I)\]
对于第 $j$ 个分量： $p(z_j) = \frac{1}{\sqrt{2\pi}} e^{-\frac{z_j^2}{2}}$
变分后验 $q(z|x)$ 是对角高斯分布：
\[q(z|x) = \mathcal{N}(\mu, \sigma^2 I)\]
对于第 $j$ 个分量： $q(z_j) = \frac{1}{\sqrt{2\pi\sigma_j^2}} e^{-\frac{(z_j-\mu_j)^2}{2\sigma_j^2}}$

由于各维度独立，我们只需要推导一维的情况，最后求和即可。根据 KL 散度的定义：

\[D_{\mathrm{KL}}(q \| p) = \int q(z) \ln \frac{q(z)}{p(z)} dz = \mathbb{E}_{z \sim q} [ \ln q(z) - \ln p(z) ]\] \[\ln q(z) = \ln \left( \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(z-\mu)^2}{2\sigma^2}} \right) = -\frac{1}{2}\ln(2\pi) - \ln\sigma - \frac{(z-\mu)^2}{2\sigma^2}\] \[\ln p(z) = \ln \left( \frac{1}{\sqrt{2\pi}} e^{-\frac{z^2}{2}} \right) = -\frac{1}{2}\ln(2\pi) - \frac{z^2}{2}\] \[\ln q(z) - \ln p(z) = -\frac{1}{2}\ln \sigma^2 - \frac{(z-\mu)^2}{2\sigma^2} + \frac{z^2}{2}\]

取期望 $\mathbb{E}_{z \sim q}[\cdot]$

我们需要对上述三项分别求期望。注意此时 $z$ 服从 $q(z) = \mathcal{N}(\mu, \sigma^2 I)$。

\[\mathbb{E}[-\frac{1}{2}\ln \sigma^2] = -\frac{1}{2}\ln \sigma^2\]
利用方差定义 $\mathbb{E}[(z-\mu)^2] = \text{Var}(z) = \sigma^2$
\[\mathbb{E}\left[ -\frac{(z-\mu)^2}{2\sigma^2} \right] = -\frac{1}{2\sigma^2} \underbrace{\mathbb{E}[(z-\mu)^2]}_{\sigma^2} = -\frac{1}{2}\]
利用公式 $\mathbb{E}[z^2] = \text{Var}(z) + (\mathbb{E}[z])^2 = \sigma^2 + \mu^2$
\[\mathbb{E}\left[ \frac{z^2}{2} \right] = \frac{1}{2} (\sigma^2 + \mu^2)\]

\[D_{\mathrm{KL}} = \frac{1}{2} \left( \sigma^2 + \mu^2 - \ln \sigma^2 - 1 \right)\]

多维求和

\[D_{\mathrm{KL}}(q\|p) = \frac{1}{2} \sum_{j=1}^M \left( \mu_j^2 + \sigma_j^2 - \ln \sigma_j^2 - 1 \right)\]

重构项

情况 A：假设数据服从高斯分布 (对应 MSE)

适用于实数数据（如彩色图片像素值归一化后）。

假设解码器输出均值 $\hat{x} = \text{Decoder}(z)$，并且方差固定为常数（例如 $\sigma_x^2 = 1$）。

\[p(x|z) = \frac{1}{\sqrt{2\pi}} \exp \left( - \frac{(x - \hat{x})^2}{2} \right)\]

取负对数：

\[-\log p(x|z) = \frac{(x - \hat{x})^2}{2} + \frac{1}{2}\ln(2\pi)\]

忽略常数项，我们要最小化的就是：

\[\mathcal{L}_{\text{recon}} \propto \frac{1}{2} (x - \hat{x})^2\]

情况 B：假设数据服从伯努利分布 (对应 BCE)

适用于二值数据（黑白图，0或1）或灰度图（视为概率）。

假设解码器输出概率 $y = \text{Sigmoid}(\text{Decoder}(z)) \in [0, 1]$。

\[p(x|z) = y^x (1-y)^{1-x}\]

取负对数：

\[-\log p(x|z) = - \left( x \ln y + (1-x) \ln (1-y) \right)\]

E-Step 与 M-Step

EM 算法

E-Step (Expectation): 固定模型参数 $\theta$，计算隐变量的后验分布 $p(z|x, \theta)$。
M-Step (Maximization): 固定后验分布，优化参数 $\theta$ 以最大化期望对数似然。

VAE 中的对应 (Variational EM)

1. 编码器 (Inference Network) $\leftrightarrow$ E-Step

传统 E-Step 需要精确计算 $p(z|x)$。
VAE 的做法：用编码器 $q_\phi(z|x)$ 去逼近真实的后验 $p(z|x)$。
训练 $\phi$ 的过程（最小化 KL 散度）就是在寻找最佳的后验分布近似。
结论：编码器负责“推断”隐变量 $z$ 的分布，这正是 E-Step 的核心任务。

2. 解码器 (Generative Network) $\leftrightarrow$ M-Step

传统 M-Step 最大化 $\mathbb{E}_{z}[\ln p(x, z | \theta)]$
VAE 的做法：采样 $z$，然后调整解码器参数 $w$，使得 $\ln p(x|z; w)$ 最大（即重构误差最小）。
结论：解码器负责在给定 $z$ 的情况下“拟合”数据，更新生成参数，这正是 M-Step 的核心任务。

代码

  
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from torch.utils.data import DataLoader, TensorDataset


# ==========================================
# 1. 准备数据
# ==========================================
def get_data(n_samples=3200):
    X, y = make_moons(n_samples=n_samples, noise=0.05, random_state=42)
    X = (X - X.mean(axis=0)) / X.std(axis=0)
    return torch.FloatTensor(X)


# ==========================================
# 2. 定义VAE 模型
# ==========================================
class VAE(nn.Module):
    def __init__(self, input_dim=2, hidden_dim=32, latent_dim=2):
        super(VAE, self).__init__()

        # --- 编码器 ---
        self.encoder = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.LeakyReLU(0.2),  # 使用 LeakyReLU 防止梯度消失
            nn.Linear(hidden_dim, hidden_dim),
            nn.LeakyReLU(0.2),
            nn.Linear(hidden_dim, hidden_dim),
            nn.LeakyReLU(0.2),
        )
        self.fc_mu = nn.Linear(hidden_dim, latent_dim)
        self.fc_logvar = nn.Linear(hidden_dim, latent_dim)

        # --- 解码器 ---
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, hidden_dim),
            nn.LeakyReLU(0.2),
            nn.Linear(hidden_dim, hidden_dim),
            nn.LeakyReLU(0.2),
            nn.Linear(hidden_dim, hidden_dim),
            nn.LeakyReLU(0.2),
            nn.Linear(hidden_dim, input_dim),
        )

    def reparameterize(self, mu, logvar):
        if self.training:
            std = torch.exp(0.5 * logvar)
            eps = torch.randn_like(std)
            return mu + eps * std
        else:
            return mu

    def forward(self, x):
        h = self.encoder(x)
        mu = self.fc_mu(h)
        logvar = self.fc_logvar(h)
        z = self.reparameterize(mu, logvar)
        recon_x = self.decoder(z)
        return recon_x, mu, logvar


# ==========================================
# 3. 损失函数
# ==========================================
def loss_function(recon_x, x, mu, logvar, kl_weight=0.05):
    # 1. 重构损失 (MSE)
    MSE = nn.functional.mse_loss(recon_x, x, reduction="sum")

    # 2. KL 散度
    KLD = 0.5 * torch.sum(mu.pow(2) + logvar.exp() - logvar - 1)

    # 加上一个权重 kl_weight (beta)，如果不加，KL项可能会主导loss，导致后验坍塌
    return MSE + kl_weight * KLD


# ==========================================
# 4. 训练流程
# ==========================================
def train():
    BATCH_SIZE = 128
    EPOCHS = 400
    LR = 1e-3

    data = get_data()
    dataset = TensorDataset(data)
    dataloader = DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True)

    model = VAE()
    optimizer = optim.Adam(model.parameters(), lr=LR)

    model.train()
    for epoch in range(EPOCHS):
        total_loss = 0
        for (x_batch,) in dataloader:
            optimizer.zero_grad()
            recon_batch, mu, logvar = model(x_batch)
            # 动态调整或固定 KL 权重
            loss = loss_function(recon_batch, x_batch, mu, logvar, kl_weight=0.1)
            loss.backward()
            optimizer.step()
            total_loss += loss.item()

        if epoch == 0 or (epoch + 1) % 100 == 0:
            print(f"Epoch {epoch+1}/{EPOCHS}, Loss: {total_loss / len(data):.4f}")

    return model, data


# ==========================================
# 5. 可视化结果
# ==========================================
def visualize(model, original_data):
    model.eval()

    # 重构
    with torch.no_grad():
        recon_data, _, _ = model(original_data)

    # 生成
    with torch.no_grad():
        z_sample = torch.randn(2000, 2)
        generated_data = model.decoder(z_sample)

    plt.figure(figsize=(15, 5))

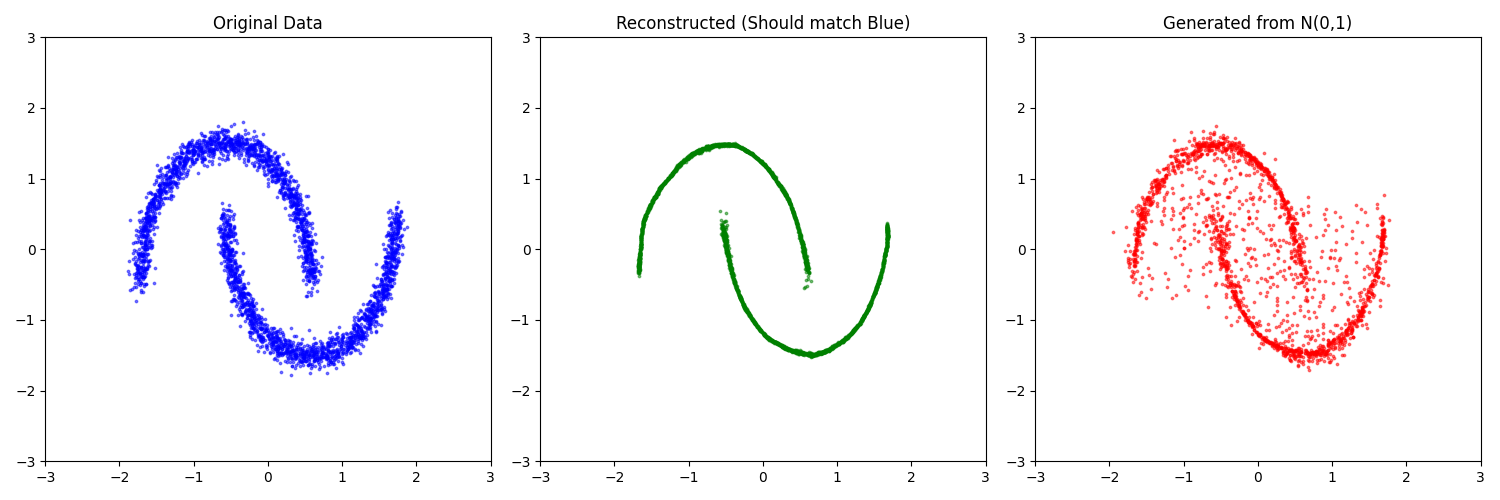
    # 1. 原始数据
    plt.subplot(1, 3, 1)
    plt.scatter(original_data[:, 0], original_data[:, 1], s=3, alpha=0.5, c="blue")
    plt.title("Original Data")
    plt.xlim(-3, 3)
    plt.ylim(-3, 3)

    # 2. 重构数据
    plt.subplot(1, 3, 2)
    plt.scatter(recon_data[:, 0], recon_data[:, 1], s=3, alpha=0.5, c="green")
    plt.title("Reconstructed (Should match Blue)")
    plt.xlim(-3, 3)
    plt.ylim(-3, 3)

    # 3. 生成数据
    plt.subplot(1, 3, 3)
    plt.scatter(generated_data[:, 0], generated_data[:, 1], s=3, alpha=0.5, c="red")
    plt.title("Generated from N(0,1)")
    plt.xlim(-3, 3)
    plt.ylim(-3, 3)

    plt.tight_layout()
    plt.savefig("1.png")


# ==========================================
# 6. 可视化插值
# ==========================================


def visualize_interpolation(model, data):
    model.eval()

    # 1. 挑选两个特定的点 (起点和终点)

    x_start = torch.FloatTensor([-1.6, 0.5]).unsqueeze(0)
    x_end = torch.FloatTensor([1.0, -1.4]).unsqueeze(0)

    # 2. 编码 (Encode) -> 拿到潜变量 z
    with torch.no_grad():
        _, mu_start, _ = model(x_start)
        _, mu_end, _ = model(x_end)

    # 3. 线性插值 (Linear Interpolation)
    steps = 30
    alphas = torch.linspace(0, 1, steps)  # 生成 0 到 1 之间的系数

    z_interpolated = []
    for alpha in alphas:
        # 公式: z = (1-alpha) * z_start + alpha * z_end
        z_point = (1 - alpha) * mu_start + alpha * mu_end
        z_interpolated.append(z_point)

    z_interpolated = torch.cat(z_interpolated, dim=0)  # 拼成一个 batch

    # 4. 解码 (Decode) -> 变回数据空间
    with torch.no_grad():
        x_interpolated = model.decoder(z_interpolated)

    # ==========================================
    # 5. 绘图
    # ==========================================
    plt.figure(figsize=(10, 8))

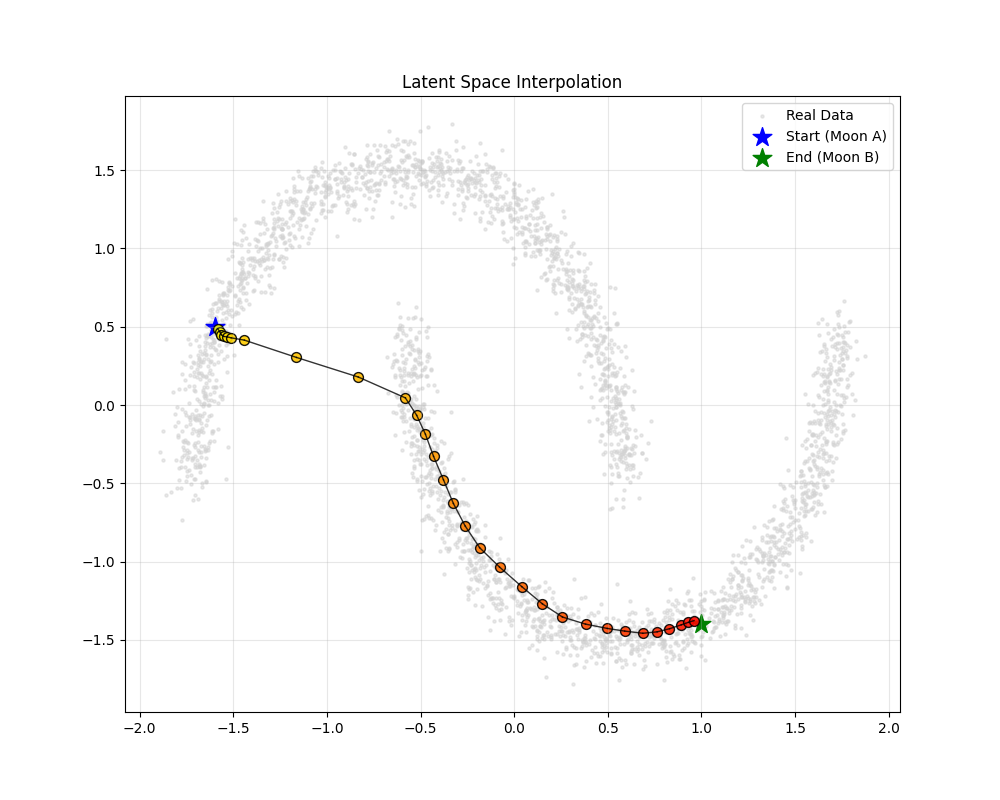
    # A. 画背景：所有真实数据 (灰色)
    plt.scatter(data[:, 0], data[:, 1], c="lightgray", s=5, alpha=0.5, label="Real Data")

    # B. 画起点和终点
    plt.scatter(x_start[:, 0], x_start[:, 1],
        c="blue", s=200, marker="*", label="Start (Moon A)")
    plt.scatter(x_end[:, 0], x_end[:, 1], c="green", s=200, marker="*", label="End (Moon B)")

    # C. 画插值轨迹 (渐变色)
    # 使用 colormap 展示时间顺序：黄色 -> 红色
    cm = plt.colormaps.get_cmap("autumn_r")

    for i in range(steps):
        color = cm(i / steps)
        # 画轨迹点
        plt.scatter(x_interpolated[i, 0], x_interpolated[i, 1],
        color=color, s=50, edgecolor="k", alpha=0.9)

        # 选画连线
        if i > 0:
            plt.plot([x_interpolated[i - 1, 0], x_interpolated[i, 0]],
                     [x_interpolated[i - 1, 1], x_interpolated[i, 1]],
            color="black", alpha=0.8, linewidth=1)

    plt.title("Latent Space Interpolation")
    plt.legend()
    plt.grid(True, alpha=0.3)
    plt.savefig("2.png")


# ==========================================
# 主程序入口
# ==========================================
if __name__ == "__main__":
    trained_model, raw_data = train()
    visualize(trained_model, raw_data)
    visualize_interpolation(trained_model, raw_data)

其他适用场景：隐马尔可夫模型（HMM）、概率PCA、因子分析、缺失数据插补等含隐变量模型的参数估计。

本文由作者按照 CC BY 4.0 进行授权

K-means算法

K-means 硬分配

K-means 的局限与 soft 思想

EM算法

问题定义

变分下界 (ELBO)

EM 算法流程

E 步（Expectation Step）

M 步（Maximization Step）

收敛性：单调有界

混合高斯模型

模型定义

E 步：计算责任度 (Responsibilities)

M 步：参数更新

更新均值 $\mu_k$

更新协方差 $\Sigma_k$

更新混合系数 $\pi_k$

用 EM 框架重写 K-means

模型设定

E 步

M 步

GMM 代码

VAE

生成建模

变分推断与证据下界（ELBO）

摊销推断 (Amortized Inference)

重参数化技巧 (The Reparameterization Trick)

计算

KL 散度

重构项

情况 A：假设数据服从高斯分布 (对应 MSE)

情况 B：假设数据服从伯努利分布 (对应 BCE)

E-Step 与 M-Step

EM 算法

VAE 中的对应 (Variational EM)

代码

热门标签