扩散模型
参考资料:
随机游走
离散随机游走
考虑一个一维离散随机游走模型:粒子在每个时间步以概率 $p = \frac{1}{2}$ 向右移动步长 $\Delta x$,以概率 $1 - p = \frac{1}{2}$ 向左移动相同步长。设第 $n$ 步的位移为随机变量 $\xi_n$。
单步统计特性
- 期望: \(\mathbb{E}[\xi_n] = (+ \Delta x) \cdot \frac{1}{2} + (- \Delta x) \cdot \frac{1}{2} = 0\)
- 方差: \(\mathrm{Var}(\xi_n) = \mathbb{E}[\xi_n^2] - (\mathbb{E}[\xi_n])^2 = (\Delta x)^2\)
多步统计特性
经过 $N$ 步后,总位移为各步独立位移之和: \(X_N = \sum_{n=1}^N \xi_n\)
- 期望: \(\mathbb{E}[X_N] = \sum_{n=1}^N \mathbb{E}[\xi_n] = 0\)
方差(由独立性): \(\mathrm{Var}(X_N) = \sum_{n=1}^N \mathrm{Var}(\xi_n) = N (\Delta x)^2\)
表明典型位移尺度为 $\sqrt{N} \Delta x$。
向连续推广
为构造连续时间随机过程,考虑极限:$\Delta t \to 0$,$\Delta x \to 0$,但总时间 $T = N \Delta t$ 保持有限。
总位移方差为: \(\mathrm{Var}(X_N) = N (\Delta x)^2 = \frac{T}{\Delta t} (\Delta x)^2\)
为获得非平凡极限(既不坍缩也不发散),要求:
\[\lim_{\Delta t \to 0} \frac{(\Delta x)^2}{\Delta t} = \sigma^2\]在此尺度下,连续时间极限过程 $X(t)$ 具有:
- $\mathbb{E}[X(t)] = 0$
- $\mathrm{Var}(X(t)) = \sigma^2 t$
由 Donsker 定理(泛函中心极限定理),离散随机游走在分布上收敛于维纳过程(Wiener process)$W(t)$,即布朗运动。
因此,在任意时刻 $t$,粒子位置服从正态分布:
\[X(t) \sim \mathcal{N}(0, \sigma^2 t)\]对应的概率密度函数为:
\[p(x, t) = \frac{1}{\sigma \sqrt{2\pi t}} \exp\left(-\frac{x^2}{2 \sigma^2 t}\right)\]伊藤微积分 (Itô calculus)
布朗运动 (Brownian Motion / Wiener Process)
一个连续时间的随机过程 $W_t$ ($t \ge 0$) 如果满足以下条件,则称为布朗运动:
- 起点: $W_0 = 0$ (以概率 1)。
- 独立增量: 对于任何 $0 \le s < t$,增量 $W_t - W_s$ 独立于过去的任何状态 $W_u (u \le s)$。
- 高斯增量: $W_t - W_s \sim \mathcal{N}(0, t-s)$。即均值为 0,方差为时间差。
- 连续路径: $W_t$ 关于 $t$ 是连续函数。
性质:Quadratic Variation
在普通微积分中,如果把 $dx$ 平方,由于 $dx$ 无穷小,$(dx)^2$ 是高阶无穷小,可以忽略(为 0)。 但在随机微积分中,$(dW_t)^2$ 不能忽略。
考虑 $dW_t \approx W_{t+dt} - W_t$。根据定义,其方差为 $dt$。
\[\mathbb{E}[(dW_t)^2] = \mathbb{E}[dW_t]^2 + Var[dW_t] = dt\]虽然这是期望值,但在极限情况下(均方收敛),有一个确定的代数规则:
\[(dW_t)^2 = dt\]这意味着 $dW_t$ 的量级大约是 $\sqrt{dt}$,比 $dt$ 要大得多(因为当 $dt \to 0$ 时,$\sqrt{dt} \gg dt$)。
运算表:
- $dt \cdot dt = 0$
- $dt \cdot dW_t = 0$
- $dW_t \cdot dW_t = dt$
Itô 积分
需要定义什么是: \(I(t) = \int_0^t f(s) dW_s\)
为什么黎曼积分失效?
黎曼积分依赖于函数是有界变差的(bounded variation)。
但布朗运动的路径极其粗糙,在任何微小区间内都在剧烈震荡,其总变差是无穷大。
\[\frac{W(t+\Delta t) - W(t)}{\Delta t} \sim \frac{\mathcal{N}(0, \Delta t)}{\Delta t} = \mathcal{N}\left(0, \frac{1}{\Delta t}\right)\]当 $\Delta t \to 0$ 时,方差趋于无穷大,意味着差商不收敛到任何有限值。
$\xi(t) = \frac{dW}{dt}$ 被称为高斯白噪声。无法作为一个点态定义的函数存在,但可以用 Schwartz 分布(广义函数)严格定义。
Itô 积分的构造
我们像黎曼和一样构造离散近似。将时间区间 $[0, t]$ 分割为 $0=t_0 < t_1 < \dots < t_N = t$。
\[I_N = \sum_{i=0}^{N-1} f(\tau_i) (W_{t_{i+1}} - W_{t_i})\]关键在于评估点 $\tau_i$ 的选择:
Itô 积分 (取左端点): $\tau_i = t_i$。
\[\int f(t) dW_t \approx \sum f(t_i) (W_{t_{i+1}} - W_{t_i})\]- 鞅 (Martingale) 非预测性。在 $t_i$ 时刻做决定(比如买股票),只能基于 $t_i$ 的信息,不能基于 $t_{i+1}$ 的信息。
Stratonovich 积分 (取中点): $\tau_i = (t_i + t_{i+1})/2$。
- 它保留了普通微积分的链式法则,但不具备鞅的性质。
Itô 引理 (Itô’s Lemma/Formula)
问题描述
假设有一个随机过程 $X_t$ 满足 SDE:
\[dX_t = \mu_t dt + \sigma_t dW_t\]现在有一个函数 $f(X_t, t)$,我们想求 $df(X_t, t)$
推导
对 $f(x, t)$ 进行二阶泰勒展开:
\[df = \frac{\partial f}{\partial t} dt + \frac{\partial f}{\partial x} dX_t + \frac{1}{2} \frac{\partial^2 f}{\partial x^2} (dX_t)^2 + \dots\]现在把 $dX_t$ 代入:
\[(dX_t)^2 = (\mu_t dt + \sigma_t dW_t)^2\] \[= \mu_t^2 (dt)^2 + 2\mu_t \sigma_t (dt)(dW_t) + \sigma_t^2 (dW_t)^2 = \sigma_t^2 dt\]将 $(dX_t)^2$ 代回泰勒展开式,我们得到著名的 Itô 公式:
\[df(X_t, t) = \left( \frac{\partial f}{\partial t} + \mu_t \frac{\partial f}{\partial x} + \frac{1}{2} \sigma_t^2 \frac{\partial^2 f}{\partial x^2} \right) dt + \sigma_t \frac{\partial f}{\partial x} dW_t\]注: 相比普通微积分,多出了 $\frac{1}{2} \sigma_t^2 \frac{\partial^2 f}{\partial x^2} dt$ 这一项(Itô 校正项)。
Fokker-Planck 方程
Fokker-Planck 方程(FPE),也称为 Kolmogorov Forward Equation,描述了随机过程 $X_t$ 的概率密度函数 $p(x, t)$ 随时间演化的规律。
目标
给定 SDE:$dX_t = \mu(X_t) dt + \sigma(X_t) dW_t$
求 $p(x, t)$ 满足的偏微分方程。
测试函数
设 $\phi(x)$ 是一个任意的、光滑的、紧支集的测试函数。
考察 $\phi(X_t)$ 的期望值随时间的变化:$\frac{d}{dt} \mathbb{E}[\phi(X_t)]$。
两种方式计算期望的导数
方式 A:使用概率密度定义
期望的定义是积分:
\[\mathbb{E}[\phi(X_t)] = \int_{-\infty}^{\infty} \phi(x) p(x, t) dx\]对时间求导,把导数移进积分号(假设 $p$ 足够光滑):
\[\frac{d}{dt} \mathbb{E}[\phi(X_t)] = \int_{-\infty}^{\infty} \phi(x) \frac{\partial p(x, t)}{\partial t} dx \quad \dots (1)\]方式 B:使用 Itô 公式
首先看 $d\phi(X_t)$。根据 Itô 公式($\phi$ 不显含 $t$,所以 $\partial_t \phi = 0$):
\[d\phi(X_t) = \left( \mu(X_t) \phi'(X_t) + \frac{1}{2} \sigma^2(X_t) \phi''(X_t) \right) dt + \sigma(X_t) \phi'(X_t) dW_t\]两边取期望,并除以 $dt$。注意 $dW_t$ 项是鞅,其期望为 0(Itô 积分)。
\[\frac{d}{dt} \mathbb{E}[\phi(X_t)] = \mathbb{E} \left[ \mu(X_t) \phi'(X_t) + \frac{1}{2} \sigma^2(X_t) \phi''(X_t) \right]\]把这个期望写成关于密度 $p(x,t)$ 的积分形式:
\[\frac{d}{dt} \mathbb{E}[\phi(X_t)] = \int_{-\infty}^{\infty} \left( \mu(x) \phi'(x) + \frac{1}{2} \sigma^2(x) \phi''(x) \right) p(x, t) dx \quad \dots (2)\]分部积分
现在我们让 (1) 式和 (2) 式相等。
为了比较,我们需要把 (2) 中的导数从 $\phi$ 转移到 $p$ 上(因为 $\phi$ 是任意的,我们要消去它)。
处理第一项 $\int \mu(x) p(x,t) \phi’(x) dx$: 边界项 $[\mu p \phi]_{-\infty}^{\infty} = 0$ (因为 $\phi$ 是紧支集的)。
\[\int \mu(x) p(x,t) \phi'(x) dx = - \int \frac{\partial}{\partial x}(\mu(x) p(x,t)) \phi(x) dx\]处理第二项 $\int \frac{1}{2} \sigma^2(x) p(x,t) \phi’‘(x) dx$: 做两次分部积分,将两个导数都转移到 $\sigma^2 p$ 上。
\[\int \frac{1}{2} \sigma^2(x) p(x,t) \phi''(x) dx = \int \frac{1}{2} \frac{\partial^2}{\partial x^2}(\sigma^2(x) p(x,t)) \phi(x) dx\]将分部积分后的结果代回 (2) 式,并与 (1) 式联立:
\[\int_{-\infty}^{\infty} \phi(x) \frac{\partial p}{\partial t} dx = \int_{-\infty}^{\infty} \phi(x) \left( -\frac{\partial}{\partial x}(\mu(x) p) + \frac{1}{2} \frac{\partial^2}{\partial x^2}(\sigma^2(x) p) \right) dx\]移项整理:
\[\int_{-\infty}^{\infty} \phi(x) \left[ \frac{\partial p}{\partial t} + \frac{\partial}{\partial x}(\mu(x) p) - \frac{1}{2} \frac{\partial^2}{\partial x^2}(\sigma^2(x) p) \right] dx = 0\]由于 $\phi(x)$ 是任意函数,要使上式恒成立,中括号内的部分必须在处处为 0(变分法基本引理)。
结论
于是我们得到了 Fokker-Planck 方程:
\[\frac{\partial p(x, t)}{\partial t} = -\frac{\partial}{\partial x} [\mu(x, t) p(x, t)] + \frac{1}{2} \frac{\partial^2}{\partial x^2} [\sigma^2(x, t) p(x, t)]\]- 第一项 $-\nabla \cdot (\mu p)$ 称为漂移项 (Drift term),代表概率质量随确定性力场的流动。
- 第二项 $\frac{1}{2} \Delta (\sigma^2 p)$ 称为扩散项 (Diffusion term),代表随机噪声导致的概率扩散(变宽)。
朗之万动力学
物理意义
朗之万动力学最初用于描述悬浮在流体中的花粉颗粒(布朗运动)。颗粒受到两个力:
- 确定性力: 来源于势能场 $U(x)$,试图将颗粒推向能量低点。
- 随机力: 来源于流体分子的热碰撞,提供随机扰动。
采样问题
在贝叶斯统计和机器学习中,我们的目标是从一个概率分布 $p(x)$ 中采样。通常这个分布可以写成玻尔兹曼形式: \(p(x) = \frac{1}{Z} e^{-U(x)}\) 其中:
- $U(x)$ 是势能函数。在贝叶斯推断中,$U(x) = -\log p(x, \mathcal{D})$。
- $Z = \int e^{-U(x)} dx$ 是归一化常数(Partition Function),通常很难计算。
朗之万采样的核心思想: 构造一个随机过程,使其随时间演化的平稳分布(Stationary Distribution)恰好是目标分布 $p(x)$。
朗之万方程 (SDE)
朗之万动力学由以下 随机微分方程 (Stochastic Differential Equation, SDE) 描述:
\[dX_t = -\nabla U(X_t) dt + \sqrt{2} dW_t\]其中:
- $X_t \in \mathbb{R}^d$ 是状态变量。
- $-\nabla U(X_t)$ 是漂移项(Drift),推动 $X_t$ 向高概率区域移动。
- $W_t$ 是标准的布朗运动(Wiener Process),$dW_t \sim \mathcal{N}(0, dt \cdot I)$。
- $\sqrt{2}$ 是扩散系数(Diffusion Coefficient)。为什么是 $\sqrt{2}$?见下文证明。
平稳分布证明
需要证明:当 $t \to \infty$ 时,$X_t$ 的概率分布 $p_t(x)$ 收敛于 $p^*(x) \propto e^{-U(x)}$。
- $\mu(x) = -\nabla U(x)$
- $\sigma(x) = \sqrt{2}$ (常数)
代入刚才推导的 FPE:
\[\frac{\partial p}{\partial t} = -\nabla \cdot (-\nabla U(x) p) + \frac{1}{2} \nabla^2 ((\sqrt{2})^2 p)\] \[\frac{\partial p}{\partial t} = \nabla \cdot (p \nabla U) + \nabla^2 p\] \[\frac{\partial p}{\partial t} = \nabla \cdot (p \nabla U + \nabla p) = - \nabla \cdot \mathbf{J}\]其中 $\mathbf{J}$ 是连续性方程表示下的概率流(Probability current)。
上式即为描述朗之万动力学概率演化的方程。
我们要求解平稳分布 $p^*(x)$ ,即满足 $\frac{\partial p^*(x)}{\partial t} = 0$ 的分布。
这意味着概率流 $\mathbf{J}$ 的散度为 0。一个充分条件是 $\mathbf{J}$ 本身为 0:
\[p^*(x) \nabla U(x) + \nabla p^*(x) = 0\]我们验证目标分布 $p^*(x) = \frac{1}{Z} e^{-U(x)}$ 是否满足上式。 首先计算 $\nabla p^*(x)$:
\[\nabla p^*(x) = \nabla \left( \frac{1}{Z} e^{-U(x)} \right) = \frac{1}{Z} e^{-U(x)} (-\nabla U(x)) = -p^*(x) \nabla U(x)\]满足平稳的充分条件。
结论: 朗之万方程定义的随机过程,其唯一的平稳分布就是玻尔兹曼分布 $p(x) \propto e^{-U(x)}$。可以通过模拟这个物理过程来进行采样。
如果离散更新公式写为:
\[x_{k+1} = x_k - \underbrace{A \cdot \eta}_{\text{漂移系数}} \nabla U(x_k) + \underbrace{\sqrt{B \cdot \eta}}_{\text{噪声系数}} z_k\]其中 $z_k \sim \mathcal{N}(0, 1)$。
那么为了收敛到 $e^{-U(x)}$,必须满足:
\[\frac{\text{噪声系数}^2}{\text{漂移系数}} = \frac{( \sqrt{B} )^2}{A} = \frac{B}{A} = 2\]离散化算法
计算机无法模拟连续时间 $dt$,必须使用离散化方法。最常用的是 Euler-Maruyama 方法。
ULA (Unadjusted Langevin Algorithm)
直接离散化 SDE:
\[x_{k+1} = x_k - \eta \nabla U(x_k) + \sqrt{2\eta} z_k\]- $\eta$:步长。
$z_k \sim \mathcal{N}(0, I)$:标准高斯噪声。
- 有偏(Biased): ULA 采样的分布只是真实分布 $p(x)$ 的近似。当 $\eta \to 0$ 时偏差消失,但混合速度变慢。
其他常见等价写法:
\[x_{k+1} = x_k - \frac{\eta}{2} \nabla U(x_k) + \sqrt{\eta} z_k\]MALA (Metropolis-Adjusted Langevin Algorithm)
为了消除 ULA 的离散化误差,我们将 ULA 产生的 $x_{k+1}$ 视为 Metropolis-Hastings (MH) 算法中的提议(Proposal)。
提议: 从 $x_k$ 生成 $\tilde{x}$:
\[\tilde{x} = x_k - \eta \nabla U(x_k) + \sqrt{2\eta} z_k\]提议分布 $q(\tilde{x} | x_k) = \mathcal{N}(\tilde{x}; x_k - \eta \nabla U(x_k), 2\eta I)$。
- 接受/拒绝: 计算接受率 $\alpha$: \(\alpha = \min \left( 1, \frac{p(\tilde{x}) q(x_k | \tilde{x})}{p(x_k) q(\tilde{x} | x_k)} \right)\)
- 更新: 以概率 $\alpha$ 接受 $\tilde{x}$,否则保持 $x_k$。
特点:
- 无偏(Unbiased): MALA 收敛到精确的 $p(x)$。
- 在高维空间中比随机游走 Metropolis (Random Walk MH) 高效得多,因为它利用了梯度信息指引方向。
能量模型
在深度生成模型中,目标是拟合数据的真实分布 $p_{data}(\mathbf{x})$。一种直观的方法是使用能量模型(Energy-Based Models, EBMs)。受统计物理启发,将概率密度函数定义为玻尔兹曼分布的形式:
\[p_\theta(\mathbf{x}) = \frac{e^{-E_\theta(\mathbf{x})}}{Z_\theta}\]其中:
- $E_\theta(\mathbf{x})$ 是由神经网络参数化的能量函数,能量越低,样本出现的概率越大。
- $Z_\theta = \int e^{-E_\theta(\mathbf{x})} d\mathbf{x}$ 是配分函数(Partition Function),用于归一化概率分布。
最大似然
通常我们通过最大化对数似然(Maximum Likelihood Estimation, MLE)来训练模型:
\[\max_\theta \mathcal{L}(\theta) = \mathbb{E}_{\mathbf{x} \sim p_{data}} [\log p_\theta(\mathbf{x})]\]我们对 $\log p_\theta(\mathbf{x})$ 关于参数 $\theta$ 求导:
\[\begin{aligned} \nabla_\theta \log p_\theta(\mathbf{x}) &= \nabla_\theta \left( -E_\theta(\mathbf{x}) - \log Z_\theta \right) \\ &= -\nabla_\theta E_\theta(\mathbf{x}) - \nabla_\theta \log \int e^{-E_\theta(\mathbf{x}')} d\mathbf{x}' \\ &= -\nabla_\theta E_\theta(\mathbf{x}) - \frac{1}{Z_\theta} \nabla_\theta \int e^{-E_\theta(\mathbf{x}')} d\mathbf{x}' \\ &= -\nabla_\theta E_\theta(\mathbf{x}) - \int \frac{e^{-E_\theta(\mathbf{x}')}}{Z_\theta} \nabla_\theta (-E_\theta(\mathbf{x}')) d\mathbf{x}' \\ &= -\nabla_\theta E_\theta(\mathbf{x}) + \mathbb{E}_{\mathbf{x}' \sim p_\theta} [\nabla_\theta E_\theta(\mathbf{x}')] \end{aligned}\]含义:
\[\nabla_\theta \log p_\theta(\mathbf{x}) = \underbrace{-\nabla_\theta E_\theta(\mathbf{x})}_{\text{拉低真实数据能量}} + \underbrace{\mathbb{E}_{\mathbf{x}' \sim p_\theta} [\nabla_\theta E_\theta(\mathbf{x}')]}_{\text{推高模型生成样本的能量}}\]- 训练目标:通过调整 $\theta$,使得真实数据的能量低,而模型自己生成的样本能量高。
- 当模型分布 $p_\theta$ 与真实数据分布完全一致时,这两项期望相等,梯度为零 —— 达到最优。
困难所在:
- 第二项需要从模型 $p_\theta$ 中采样(例如用 MCMC),这在高维空间中计算昂贵,是 EBM 训练的主要难点。
- 实践中常使用近似方法(如对比散度、噪声对比估计等)。
Score Function
为了避开 $Z_\theta$,我们转而关注关于输入 $\mathbf{x}$ 的梯度,而非参数 $\theta$ 的梯度。定义 Stein Score Function 为:
\[s_\theta(\mathbf{x}) = \nabla_\mathbf{x} \log p_\theta(\mathbf{x}) = \nabla_\mathbf{x} (-E_\theta(\mathbf{x}) - \log Z_\theta) = -\nabla_\mathbf{x} E_\theta(\mathbf{x})\]Denoising Score Matching (DSM)
数据分布
我们的目标是训练神经网络 $s_\theta(\mathbf{x})$ 逼近真实数据的 Score $\nabla_\mathbf{x} \log p_{data}(\mathbf{x})$。最直观的目标是最小化 Fisher Divergence:
\[\mathcal{L}_{SM} = \frac{1}{2} \mathbb{E}_{p_{data}} \left[ \| s_\theta(\mathbf{x}) - \nabla_\mathbf{x} \log p_{data}(\mathbf{x}) \|^2_2 \right]\]经验分布
设我们有训练数据集 ${ \mathbf{x}^{(1)}, \dots, \mathbf{x}^{(N)} } \subset \mathbb{R}^d$,其经验分布为:
\[p_{\text{data}}(\mathbf{x}) = \frac{1}{N} \sum_{i=1}^N \delta(\mathbf{x} - \mathbf{x}^{(i)})\]其中 $\delta(\cdot)$ 是 Dirac delta 函数。
问题:该分布在支撑集(support)之外为零,在支撑集上不可导(甚至不连续),因此其 score $\nabla_{\mathbf{x}} \log p_{\text{data}}(\mathbf{x})$ 几乎处处无定义。
平滑化
为使分布可微,我们对经验分布进行平滑,即与一个光滑核函数 $k_\sigma(\tilde{\mathbf{x}} | \mathbf{x})$ 卷积:
\[q_\sigma(\tilde{\mathbf{x}}) := (p_{\text{data}} * k_\sigma)(\tilde{\mathbf{x}}) = \int k_\sigma(\tilde{\mathbf{x}} | \mathbf{x}) p_{\text{data}}(\mathbf{x}) \, d\mathbf{x} = \frac{1}{N} \sum_{i=1}^N k_\sigma(\tilde{\mathbf{x}} | \mathbf{x}^{(i)})\]这正是 Parzen 窗估计(或核密度估计,KDE)。
最常见的选择是各向同性高斯核:
\[k_\sigma(\tilde{\mathbf{x}} | \mathbf{x}) = \mathcal{N}(\tilde{\mathbf{x}}; \mathbf{x}, \sigma^2 \mathbf{I}) = \frac{1}{(2\pi \sigma^2)^{d/2}} \exp\left( -\frac{\| \tilde{\mathbf{x}} - \mathbf{x} \|^2}{2\sigma^2} \right)\]于是,平滑后的密度为:
\[q_\sigma(\tilde{\mathbf{x}}) = \frac{1}{N} \sum_{i=1}^N \mathcal{N}(\tilde{\mathbf{x}}; \mathbf{x}^{(i)}, \sigma^2 \mathbf{I})\]该函数处处光滑、正定、可微,其 score $\nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}})$ 有良好定义。
平滑分布的 Score
我们希望训练一个神经网络 $s_\theta(\tilde{\mathbf{x}})$ 来逼近: \(\nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}})\)
但直接计算此损失仍困难,因为 $q_\sigma(\tilde{\mathbf{x}})$ 是混合高斯,其 score 涉及归一化常数。
\[\nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}}) = \frac{\nabla_{\tilde{\mathbf{x}}} q_\sigma(\tilde{\mathbf{x}})}{q_\sigma(\tilde{\mathbf{x}})} = \frac{\sum_i \nabla_{\tilde{\mathbf{x}}} k(\tilde{\mathbf{x}}|\mathbf{x}^{(i)})}{\sum_j k(\tilde{\mathbf{x}}|\mathbf{x}^{(j)})}\]要计算这个梯度,每次都需要遍历整个数据集(求和 $\sum$),这在数据量巨大时是不可行的。
Denoising Score Matching
Vincent (2011) 提出的 DSM 巧妙地绕过了计算 $\nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}})$ 的需求。
定理陈述
最小化关于平滑后边缘分布 $q_\sigma(\tilde{\mathbf{x}})$ 的 Score Matching 损失:
\[\mathcal{L}_{SM} = \frac{1}{2} \mathbb{E}_{\tilde{\mathbf{x}} \sim q_\sigma} \left[ \| s_\theta(\tilde{\mathbf{x}}) - \nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}}) \|^2 \right]\]等价于最小化关于条件加噪分布 $k_\sigma(\tilde{\mathbf{x}}|\mathbf{x})$ 的 Denoising 损失:
\[\mathcal{L}_{DSM} = \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{data}, \tilde{\mathbf{x}} \sim k_\sigma(\cdot|\mathbf{x})} \left[ \| s_\theta(\tilde{\mathbf{x}}) - \nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) \|^2 \right] + C\]理解:不需要让模型去预测复杂的混合分布的梯度(边缘 score),只需要让模型去预测“如果是从 $\mathbf{x}$ 加噪得到的 $\tilde{\mathbf{x}}$,那么噪声梯度的反方向在哪里”(条件 score)。
第一步:展开 $\mathcal{L}_{SM}$
\(\begin{aligned} \mathcal{L}_{SM} &= \frac{1}{2} \mathbb{E}_{\tilde{\mathbf{x}} \sim q_\sigma} \left[ \| s_\theta(\tilde{\mathbf{x}}) - \nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}}) \|^2 \right] \\ &= \frac{1}{2} \mathbb{E}_{q_\sigma} \left[ \| s_\theta(\tilde{\mathbf{x}}) \|^2 \right] - \underbrace{\mathbb{E}_{q_\sigma} \left[ s_\theta(\tilde{\mathbf{x}})^T \nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}}) \right]}_{\text{交叉项}} + \underbrace{\frac{1}{2} \mathbb{E}_{q_\sigma} [ \| \nabla \log q_\sigma \|^2 ]}_{\text{常数 (与 } \theta \text{ 无关)}} \end{aligned}\)
第二步:处理交叉项
\[\begin{aligned} \text{Cross Term} &= \int q_\sigma(\tilde{\mathbf{x}}) s_\theta(\tilde{\mathbf{x}})^T \nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}}) d\tilde{\mathbf{x}} \\ &= \int q_\sigma(\tilde{\mathbf{x}}) s_\theta(\tilde{\mathbf{x}})^T \frac{\nabla_{\tilde{\mathbf{x}}} q_\sigma(\tilde{\mathbf{x}})}{q_\sigma(\tilde{\mathbf{x}})} d\tilde{\mathbf{x}} \\ &= \int s_\theta(\tilde{\mathbf{x}})^T \nabla_{\tilde{\mathbf{x}}} q_\sigma(\tilde{\mathbf{x}}) d\tilde{\mathbf{x}} \end{aligned}\]代入 $q_\sigma(\tilde{\mathbf{x}})$ 的定义 $q_\sigma(\tilde{\mathbf{x}}) = \int p_{data}(\mathbf{x}) k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) d\mathbf{x}$ ,并利用 $\nabla$ 对积分的线性性质(交换积分与微分):
\[\begin{aligned} \text{Cross Term} &= \int s_\theta(\tilde{\mathbf{x}})^T \nabla_{\tilde{\mathbf{x}}} \left( \int p_{data}(\mathbf{x}) k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) d\mathbf{x} \right) d\tilde{\mathbf{x}} \\ &= \int s_\theta(\tilde{\mathbf{x}})^T \left( \int p_{data}(\mathbf{x}) \nabla_{\tilde{\mathbf{x}}} k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) d\mathbf{x} \right) d\tilde{\mathbf{x}} \end{aligned}\]再次利用恒等式 $\nabla k = k \nabla \log k$:
\[\begin{aligned} \text{Cross Term} &= \int \int p_{data}(\mathbf{x}) s_\theta(\tilde{\mathbf{x}})^T \left( k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) \nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) \right) d\mathbf{x} d\tilde{\mathbf{x}} \\ &= \int \int p_{data}(\mathbf{x}) k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) \left[ s_\theta(\tilde{\mathbf{x}})^T \nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) \right] d\mathbf{x} d\tilde{\mathbf{x}} \\ &= \mathbb{E}_{\mathbf{x} \sim p_{data}, \tilde{\mathbf{x}} \sim k_\sigma(\cdot|\mathbf{x})} \left[ s_\theta(\tilde{\mathbf{x}})^T \nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) \right] \end{aligned}\]第三步:构造 $\mathcal{L}_{DSM}$
现在来看目标损失函数 $\mathcal{L}_{DSM}$ 的展开:
\[\begin{aligned} \mathcal{L}_{DSM} &= \frac{1}{2} \mathbb{E}_{p_{data}, k_\sigma} \left[ \| s_\theta(\tilde{\mathbf{x}}) - \nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) \|^2 \right] \\ &= \frac{1}{2} \underbrace{\mathbb{E}_{p_{data}, k_\sigma} [\| s_\theta(\tilde{\mathbf{x}}) \|^2]}_{A} - \underbrace{\mathbb{E}_{p_{data}, k_\sigma} [s_\theta(\tilde{\mathbf{x}})^T \nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x})]}_{B} + C \end{aligned}\]注意到:
- 项 $A$ 中,$\tilde{\mathbf{x}}$ 的边缘分布正是 $q_\sigma$,所以 $A = \mathbb{E}_{q_\sigma} [| s_\theta(\tilde{\mathbf{x}}) |^2]$。这与 $\mathcal{L}_{SM}$ 的第一项完全相同。
- 项 $B$ 正是我们刚才推导出的 $\mathcal{L}_{SM}$ 的交叉项。
这意味着优化 $\mathcal{L}_{DSM}$ 等价于优化 $\mathcal{L}_{SM}$,但 $\mathcal{L}_{DSM}$ 中的 $\nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x})$ 具有解析解,极易计算。
高斯噪声下的具体形式
当核函数是高斯分布时:
\[k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) = \frac{1}{(2\pi\sigma^2)^{d/2}} \exp \left( - \frac{\| \tilde{\mathbf{x}} - \mathbf{x} \|^2}{2\sigma^2} \right)\]1. 计算条件 Score:
\[\log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) = - \frac{\| \tilde{\mathbf{x}} - \mathbf{x} \|^2}{2\sigma^2} + C\] \[\nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) = - \frac{\tilde{\mathbf{x}} - \mathbf{x}}{\sigma^2}\]2. 重参数化技巧 (Reparameterization Trick):
采样 $\tilde{\mathbf{x}} \sim k_\sigma(\cdot|\mathbf{x})$ 等价于:
\[\tilde{\mathbf{x}} = \mathbf{x} + \sigma \boldsymbol{\epsilon}, \quad \text{其中 } \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\]此时条件 Score 变为:
\[\nabla_{\tilde{\mathbf{x}}} \log k_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) = - \frac{(\mathbf{x} + \sigma \boldsymbol{\epsilon}) - \mathbf{x}}{\sigma^2} = - \frac{\boldsymbol{\epsilon}}{\sigma}\]3. 最终损失函数:
代入 $\mathcal{L}_{DSM}$:
\[\begin{aligned} \mathcal{L}_{DSM}(\theta) &= \frac{1}{2} \mathbb{E}_{\mathbf{x}, \boldsymbol{\epsilon}} \left[ \left( s_\theta(\mathbf{x} + \sigma \boldsymbol{\epsilon}) - \left( -\frac{\boldsymbol{\epsilon}}{\sigma} \right) \right)^2 \right] \\ &= \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{data}, \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})} \left[ (s_\theta(\mathbf{x} + \sigma \boldsymbol{\epsilon}) + \frac{\boldsymbol{\epsilon}}{\sigma}) ^2 \right] \end{aligned}\]模型 $s_\theta$ 被训练去预测负的标准化噪声。即模型在学习去噪(Denoising)。它看到带噪图像,试图指出“回到干净图像的方向”。
Denoising Score Matching (DSM): 最优估计视角
目标
目标是训练一个神经网络 $s_\theta(x, t)$ 来逼近数据在任意时刻 $t$ 的边缘分布分数(Marginal Score):
\[s_t(x) = \nabla_x \log p_t(x)\]其中 $p_t(x)$ 是真实数据 $x_0$ 经过扩散过程(加噪)后的边缘分布。
难点:直接计算 $p_t(x) = \int p(x|x_0)p_{\text{data}}(x_0) dx_0$ 及其梯度通常是不可行的,因为它涉及对高维数据分布的积分。
分数与其条件期望
虽然边缘分数 $\nabla_x \log p_t(x)$ 难以计算,但有一个重要的恒等式,将边缘分数与条件分数(Conditional Score)联系起来:
\[\nabla_x \log p_t(x) = \mathbb{E}_{p(x_0 \mid x_t)} \left[ \nabla_x \log p(x_t \mid x_0) \mid x_t = x \right]\]当前时刻 $x$ 的分数 等于 所有可能产生 $x$ 的初始点 $x_0$ 对应的条件分数的期望。
最优估计原理 (MMSE)
最小均方误差(Minimum Mean Square Error, MMSE)估计原理:
\[\hat{Y}^*(X) = \mathbb{E}[Y \mid X]\]定理:对于任意随机变量 $Y$ 和观测变量 $X$,使得均方误差 $\mathbb{E}[|\hat{Y}(X) - Y|^2]$ 最小化的估计器 $\hat{Y}(X)$ 是 $Y$ 的后验期望,即:
将此原理应用到分数匹配中:
- 观测变量 (Input):$X = x_t$(带噪图像)
- 目标变量 (Target):$Y = \nabla_{x_t} \log p(x_t \mid x_0)$(条件分数)
- 估计器 (Model):$\hat{Y} = s_\theta(x_t, t)$
根据定理,如果优化以下回归损失:
\[\min_\theta \mathbb{E}_{x_0, x_t} \left[ \left\| s_\theta(x_t, t) - \nabla_{x_t} \log p(x_t \mid x_0) \right\|^2 \right]\]那么最优解 $s_{\theta^*}(x, t)$ 将收敛到目标变量的期望:
\[s_{\theta^*}(x, t) = \mathbb{E}[\nabla_{x_t} \log p(x_t \mid x_0) \mid x_t = x] = \nabla_x \log p_t(x)\]不需要直接根据边缘分布去计算梯度,只需要让模型去回归如果是从 $x_0$ 变过来的,现在的梯度应该是多少。
高斯过程下的解析解
在扩散模型中,前向过程通常是高斯的:
\[p(x_t \mid x_0) = \mathcal{N}(x_t; \alpha(t) x_0,\, \sigma^2(t) I)\]利用重参数化技巧(Reparameterization Trick),采样过程可写为:
\[x_t = \alpha(t) x_0 + \sigma(t) \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)\]计算条件分数(Target $Y$):
高斯分布的对数密度为:
\[\log p(x_t \mid x_0) = -\frac{1}{2\sigma^2(t)} \| x_t - \alpha(t) x_0 \|^2 + C\]对 $x_t$ 求梯度:
\[\nabla_{x_t} \log p(x_t \mid x_0) = -\frac{x_t - \alpha(t) x_0}{\sigma^2(t)}\]代入 $x_t - \alpha(t)x_0 = \sigma(t)\epsilon$:
\[\nabla_{x_t} \log p(x_t \mid x_0) = -\frac{\sigma(t)\epsilon}{\sigma^2(t)} = \boxed{-\frac{\epsilon}{\sigma(t)}}\]构建 DSM 损失函数
将上述结果代入 MMSE 损失函数:
\[\mathcal{L}_{\text{DSM}}(\theta) = \mathbb{E}_{t, x_0, \epsilon} \left[ \left\| s_\theta(x_t, t) - \left( -\frac{\epsilon}{\sigma(t)} \right) \right\|^2 \right]\]噪声预测参数化 (Noise Prediction)
为了数值稳定性和实现简单,我们通常不直接让网络输出分数,而是让网络预测噪声 $\epsilon_\theta(x_t, t)$。 定义网络输出与分数的关系为:
\[s_\theta(x_t, t) := -\frac{\epsilon_\theta(x_t, t)}{\sigma(t)}\]代入损失函数:
\[\begin{aligned} \mathcal{L}_{\text{DSM}}(\theta) &= \mathbb{E} \left[ \left\| -\frac{\epsilon_\theta(x_t, t)}{\sigma(t)} - \left( -\frac{\epsilon}{\sigma(t)} \right) \right\|^2 \right] \\ &= \mathbb{E} \left[ \frac{1}{\sigma^2(t)} \| \epsilon - \epsilon_\theta(x_t, t) \|^2 \right] \end{aligned}\]在 DDPM 等实践中,通常会忽略权重系数 $1/\sigma^2(t)$(这相当于对不同时间步加权),得到最终的简化损失函数:
\[\mathcal{L}_{\text{simple}}(\theta) = \mathbb{E}_{t \sim \mathcal{U}, x_0 \sim p_{\text{data}}, \epsilon \sim \mathcal{N}(0,I)} \left[ \left\| \epsilon - \epsilon_\theta(\underbrace{\alpha(t)x_0 + \sigma(t)\epsilon}_{x_t}, t) \right\|^2 \right]\]扩散模型 (Diffusion Models)
扩散模型的前向过程是将数据加噪变成高斯分布。 生成过程(反向过程)就是求解一个反向时间的朗之万类型的 SDE。
宋飏 (Yang Song) 等人提出的 Score-based Generative Modeling 框架中,生成样本的过程就是:
\[dX_t = [\dots \nabla \log p_t(X_t)] dt + d\bar{W}_t\]也就是训练一个神经网络去估计 $\nabla \log p_t(x)$(Score Matching),然后把这个网络代入朗之万动力学方程中,从纯噪声开始迭代,最终去噪得到图像。
Annealed Langevin Dynamics:
为了解决朗之万动力学在低密度区域混合慢的问题,现代方法会在采样初期使用大噪声平滑分布,随着采样进行逐渐减小噪声(退火)。使用一系列噪声尺度:
\[\sigma_1 < \sigma_2 < \dots < \sigma_T\]Variance Preserving (VP) SDE
在 Ho et al. (2020) DDPM 论文中,前向加噪过程是离散的马尔可夫链:
\[\mathbf{x}_{k} = \sqrt{1 - \beta_k} \mathbf{x}_{k-1} + \sqrt{\beta_k} \mathbf{z}_{k-1}, \quad \mathbf{z} \sim \mathcal{N}(0, \mathbf{I})\]这里 $\beta_k$ 是一个很小的数(比如 0.0001)。
重写离散方程,表示为增量形式:
\[\mathbf{x}_k - \mathbf{x}_{k-1} = (\sqrt{1 - \beta_k} - 1) \mathbf{x}_{k-1} + \sqrt{\beta_k} \mathbf{z}_{k-1}\]当 $\beta_k$ 趋于无穷小时,使用泰勒展开 $\sqrt{1 - \beta_k} \approx 1 - \frac{1}{2}\beta_k$:
离散方程近似为:
\[\Delta \mathbf{x} \approx -\frac{1}{2} \beta_k \mathbf{x} + \sqrt{\beta_k} \mathbf{z}\]如果定义连续时间变量 $t$,并设 $\beta_k = \beta(t) \Delta t$
得到 VP-SDE:
\[d\mathbf{X}_t = -\frac{1}{2} \beta(t) \mathbf{X}_t dt + \sqrt{\beta(t)} d\mathbf{W}_t\]VP-SDE前向过程可以看作 $U(x) = x$ 的物理系统,其平稳态恰好是标准正态分布。即随着时间 $t \to \infty$,分布 $p_t(\mathbf{x})$ 将收敛到 标准正态分布 $\mathcal{N}(\mathbf{0}, \mathbf{I})$。
Variance Exploding (VE) SDE
VE-SDE 的前向过程没有漂移项(不试图把数据拉向原点),而是简单地不断注入越来越大的噪声,直到原始数据的分布被巨大的噪声完全淹没。
前向 SDE 形式为:
\[d\mathbf{x} = \sqrt{\frac{d[\sigma^2(t)]}{dt}} d\mathbf{w} = g(t) d\mathbf{w}\]其中 $\sigma(t)$ 是噪声标准差的调度函数。
扰动核 (Perturbation Kernel)
由于没有漂移项,给定时刻 $t$ 的条件分布(扰动核)非常简单:
\[p_{0t}(\mathbf{x}(t) | \mathbf{x}(0)) = \mathcal{N}(\mathbf{x}(t); \mathbf{x}(0), [\sigma^2(t) - \sigma^2(0)] \mathbf{I})\]通常假设 $\sigma(0) \approx 0$,则有:
\[\mathbf{x}(t) \approx \mathbf{x}(0) + \sigma(t) \mathbf{z}, \quad \mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\]噪声调度 (Noise Schedule)
VE-SDE 的标准做法:使用几何级数来安排 $\sigma(t)$。
\[\sigma(t) = \sigma_{\min} \left( \frac{\sigma_{\max}}{\sigma_{\min}} \right)^t, \quad t \in [0, 1]\]对应的扩散系数 $g(t)$ 为:
\[g(t) = \sqrt{\frac{d\sigma^2(t)}{dt}} = \sigma(t) \sqrt{2 \ln \left( \frac{\sigma_{\max}}{\sigma_{\min}} \right)}\]训练目标 (Loss)
在 VE-SDE 下,Score Matching 的目标函数通常会乘以 $\sigma(t)^2$ 来平衡不同噪声等级下的损失权重:
\[\mathcal{L} = \mathbb{E}_{t, \mathbf{x}(0), \mathbf{z}} \left[ \left\| \sigma(t) s_\theta(\mathbf{x}(t), t) + \mathbf{z} \right\|_2^2 \right]\]Time Reversal of Diffusions
给定前向过程的 SDE:
\[d\mathbf{X}_t = \boldsymbol{\mu}(\mathbf{X}_t, t) dt + \boldsymbol{\sigma}(t) d\mathbf{W}_t\]其对应的反向过程由以下 SDE 描述:
\[\boxed{ d\mathbf{X}_t = \left[ \boldsymbol{\mu}(\mathbf{X}_t, t) - \boldsymbol{\sigma}(t)^2 \nabla_{\mathbf{X}_t} \log p_t(\mathbf{X}_t) \right] dt + \boldsymbol{\sigma}(t) d\mathbf{\bar{W}}_t }\]其中 \(d\mathbf{\bar{W}}_t\) 是一个反向的维纳过程。
VP-SDE 的反向过程:
\[d\mathbf{X}_t = \left[ - \frac{1}{2} \beta(t) \mathbf{X}_t - \beta(t) \nabla_{\mathbf{X}_t} \log p_t(\mathbf{X}_t) \right] dt + \sqrt{\beta(t)} d\mathbf{\bar{W}}_t\]VE-SDE 的反向过程:
\[d\mathbf{x}_t = \left[ \mathbf{0} - g(t)^2 \nabla_{\mathbf{x}} \log p_t(\mathbf{x}) \right] dt + g(t) d\mathbf{\bar{w}}\]证明: 反向过程
前向 Fokker-Planck 方程
根据前向 SDE,概率密度函数 $p(\mathbf{x}, t)$ 随时间的演化满足 Fokker-Planck 方程:
\[\frac{\partial p}{\partial t} = -\nabla \cdot (\boldsymbol{\mu} p) + \frac{1}{2} \sigma^2 \nabla^2 p \quad \dots (1)\]这里 $\nabla \cdot$ 是散度,$\nabla^2$ 是拉普拉斯算子。
反向时间的演化
我们定义反向时间变量 $\tau = T - t$。我们希望找到一个关于 $\tau$ 的随机过程,使得其概率密度演化与原过程在时间倒流时一致。 根据链式法则,密度随反向时间的变化率为:
\[\frac{\partial p}{\partial \tau} = \frac{\partial p}{\partial t} \frac{dt}{d\tau} = - \frac{\partial p}{\partial t}\]将 (1) 式代入:
\[\frac{\partial p}{\partial \tau} = \nabla \cdot (\boldsymbol{\mu} p) - \frac{1}{2} \sigma^2 \nabla^2 p \quad \dots (2)\]目标是把 (2) 式重写成一个标准的 Fokker-Planck 方程的形式。
构造反向 Fokker-Planck 形式
标准的 Fokker-Planck 方程形式为: \(\frac{\partial p}{\partial \tau} = -\nabla \cdot (\boldsymbol{\mu}_{rev} p) + \frac{1}{2} \sigma^2 \nabla^2 p\)
其中 $\boldsymbol{\mu}_{rev}$ 是我们要寻找的反向漂移项。
FPE 的扩散项必须是正的($+\frac{1}{2}\sigma^2 \nabla^2 p$);而 (2) 式中是负的。
关键恒等式:Score Function
利用 $\nabla p = p \nabla \log p$,我们可以将拉普拉斯项 $\nabla^2 p = \nabla \cdot (\nabla p)$ 重写:
\[\nabla^2 p = \nabla \cdot (p \nabla \log p)\]在 (2) 式右边加上并减去 $\sigma^2 \nabla^2 p$:
\[\begin{aligned} \frac{\partial p}{\partial \tau} &= \nabla \cdot (\boldsymbol{\mu} p) - \frac{1}{2} \sigma^2 \nabla^2 p \\ &= \nabla \cdot (\boldsymbol{\mu} p) - \sigma^2 \nabla^2 p + \frac{1}{2} \sigma^2 \nabla^2 p \\ \end{aligned}\] \[\begin{aligned} \text{前两项} &= \nabla \cdot (\boldsymbol{\mu} p) - \sigma^2 \nabla \cdot (p \nabla \log p) \\ &= \nabla \cdot \left( \boldsymbol{\mu} p - \sigma^2 p \nabla \log p \right) \\ &= \nabla \cdot \left( [ \boldsymbol{\mu} - \sigma^2 \nabla \log p ] p \right) \\ &= -\nabla \cdot \left( \underbrace{[ -\boldsymbol{\mu} + \sigma^2 \nabla \log p ]}_{\boldsymbol{\mu}_{rev}} p \right) \end{aligned}\]得到反向时间的演化方程:
\[\frac{\partial p}{\partial \tau} = -\nabla \cdot \left( \left[ -\boldsymbol{\mu} + \sigma^2 \nabla \log p \right] p \right) + \frac{1}{2} \sigma^2 \nabla^2 p\]反向 SDE 的参数:
- 反向扩散系数:$\sigma(t)$ (保持不变)
- 反向漂移系数: \(\boldsymbol{\mu}_{rev}(\mathbf{X}_t, t) = -\boldsymbol{\mu}(\mathbf{X}_t, t) + \sigma(t)^2 \nabla_{\mathbf{X}_t} \log p_t(\mathbf{X}_t)\)
证明: 反向过程(离散时间推导)
考虑一个很小的时间步长 \(\Delta t\)。
前向转移概率
从 \(\mathbf{X}_t\) 到 \(\mathbf{X}_{t+\Delta t}\) 的转移可以写成:
\[\mathbf{X}_{t+\Delta t} \approx \mathbf{X}_t + \boldsymbol{\mu}(\mathbf{X}_t, t) \Delta t + \boldsymbol{\sigma}(t) \sqrt{\Delta t} \mathbf{z}\]其中 \(\mathbf{z} \sim \mathcal{N}(0, \mathbf{I})\)。
这说明,给定 \(\mathbf{X}_t\),\(\mathbf{X}_{t+\Delta t}\) 的条件概率是一个高斯分布:
\[p(\mathbf{X}_{t+\Delta t} | \mathbf{X}_t) = \mathcal{N}(\mathbf{X}_{t+\Delta t}; \mathbf{X}_t + \boldsymbol{\mu}(\mathbf{X}_t, t)\Delta t, \boldsymbol{\sigma}(t)^2 \Delta t)\]反向转移概率
我们想要求的是反向的转移概率 \(p(\mathbf{X}_t | \mathbf{X}_{t+\Delta t})\) 。根据贝叶斯定理:
\[p(\mathbf{X}_t | \mathbf{X}_{t+\Delta t}) = \frac{p(\mathbf{X}_{t+\Delta t} | \mathbf{X}_t) p_t(\mathbf{X}_t)}{p_{t+\Delta t}(\mathbf{X}_{t+\Delta t})}\]取对数:
\[\log p(\mathbf{X}_t | \mathbf{X}_{t+\Delta t}) = \log p(\mathbf{X}_{t+\Delta t} | \mathbf{X}_t) + \log p_t(\mathbf{X}_t) - \log p_{t+\Delta t}(\mathbf{X}_{t+\Delta t})\]第一项: \(\log p(\mathbf{X}_{t+\Delta t} | \mathbf{X}_t) = C_1 - \frac{1}{2 \boldsymbol{\sigma}(t)^2 \Delta t} ||\mathbf{X}_{t+\Delta t} - (\mathbf{X}_t + \boldsymbol{\mu}(\mathbf{X}_t, t)\Delta t)||^2\)
后两项: 我们对 \(\log p_{t+\Delta t}(\mathbf{X}_{t+\Delta t})\) 在 \((\mathbf{X}_t, t)\) 处一阶泰勒展开(忽略了高阶无穷小): \(\begin{aligned} \log p_{t+\Delta t}(\mathbf{X}_{t+\Delta t}) &\approx \log p_t(\mathbf{X}_t) + \frac{\partial \log p_t}{\partial t} \Delta t + (\mathbf{X}_{t+\Delta t} - \mathbf{X}_t)^T \nabla_{\mathbf{X}_t} \log p_t(\mathbf{X}_t) \\ \implies \log p_t(\mathbf{X}_t) - \log p_{t+\Delta t}(\mathbf{X}_{t+\Delta t}) &\approx - \frac{\partial \log p_t}{\partial t} \Delta t - (\mathbf{X}_{t+\Delta t} - \mathbf{X}_t)^T \nabla_{\mathbf{X}_t} \log p_t(\mathbf{X}_t) \end{aligned}\) 将展开式代入 \(\log p(\mathbf{X}_t | \mathbf{X}_{t+\Delta t})\)
我们只关心与 \(\mathbf{X}_t\) 相关的项,因为我们想得到一个关于 \(\mathbf{X}_t\) 的高斯分布。
\[\log p(\mathbf{X}_t | \mathbf{X}_{t+\Delta t}) \approx C - \frac{1}{2 \sigma^2 \Delta t} ||\mathbf{X}_{t+\Delta t} - \mathbf{X}_t - \boldsymbol{\mu} \Delta t||^2 - (\mathbf{X}_{t+\Delta t} - \mathbf{X}_t)^T \nabla \log p_t\]展开二次项,保留与 \(\mathbf{X}_t\) 相关的主导项:
\[\approx C' - \frac{1}{2 \sigma^2 \Delta t} (\mathbf{X}_t^T\mathbf{X}_t - 2 \mathbf{X}_t^T(\mathbf{X}_{t+\Delta t} - \boldsymbol{\mu}\Delta t)) + \mathbf{X}_t^T \nabla \log p_t\]我们对方程进行配方,使其形式为 \(-\frac{1}{2\text{Var}} ||\mathbf{X}_t - \text{Mean}||^2\)。 通过整理关于 \(\mathbf{X}_t\) 的一次项和二次项,可以发现这个分布是一个均值为 \(\mathbf{X}_{t+\Delta t} - \boldsymbol{\mu}_{rev} \Delta t\),方差为 \(\sigma^2 \Delta t\) 的高斯分布。
经过一些代数运算,可以推导出反向漂移项 \(\boldsymbol{\mu}_{rev}\) 满足:
\[\boldsymbol{\mu}_{rev}(\mathbf{X}_t, t) \approx \boldsymbol{\mu}(\mathbf{X}_t, t) - \boldsymbol{\sigma}(t)^2 \nabla_{\mathbf{X}_t} \log p_t(\mathbf{X}_t)\]由于这个推导是针对从 \(t+\Delta t\) 到 \(t\) 的过程,时间在减少。如果我们定义反向 SDE 的时间是向前流逝的(即 \(dt\) 为正),那么漂移项需要取反。因此,反向过程的漂移项为:
\[\boldsymbol{\mu}_{reverse} = - \boldsymbol{\mu}_{rev} = -\boldsymbol{\mu}(\mathbf{X}_t, t) + \boldsymbol{\sigma}(t)^2 \nabla_{\mathbf{X}_t} \log p_t(\mathbf{X}_t)\]Probability Flow ODE
存在一个常微分方程(ODE),其对应的概率密度演化与原始随机微分方程(SDE)完全一致:即在任意时刻 $t$,二者具有相同的边缘概率密度 $p(\mathbf{x}, t)$。
前向 SDE
\[d\mathbf{x} = \boldsymbol{\mu}(\mathbf{x}, t)\, dt + \sigma(t)\, d\mathbf{w}\]该 SDE 对应的概率密度 $p(\mathbf{x}, t)$ 满足:
\[\frac{\partial p}{\partial t} = -\nabla \cdot (\boldsymbol{\mu} p) + \frac{1}{2} \sigma^2(t) \nabla^2 p \quad \dots (1)\]目标是将 (1) 式重写为连续性方程的形式:
\[\frac{\partial p}{\partial t} + \nabla \cdot (\tilde{\boldsymbol{\mu}} p) = 0\]这对应于一个确定性动力系统:
\[\frac{d\mathbf{x}}{dt} = \tilde{\boldsymbol{\mu}}(\mathbf{x}, t)\]为此,利用 score function 恒等式 $\nabla p = p \nabla \log p$,将扩散项重写为:
\[\nabla^2 p = \nabla \cdot (\nabla p) = \nabla \cdot (p \nabla \log p)\]代入 (1) 式:
\[\begin{aligned} \frac{\partial p}{\partial t} &= -\nabla \cdot (\boldsymbol{\mu} p) + \frac{1}{2} \sigma^2(t) \nabla \cdot (p \nabla \log p) \\ &= -\nabla \cdot \left[ \left( \boldsymbol{\mu} - \frac{1}{2} \sigma^2(t) \nabla \log p \right) p \right] \end{aligned}\]可将其识别为连续性方程,其中等效漂移场(即 Probability Flow ODE 的向量场)为:
\[\tilde{\boldsymbol{\mu}}(\mathbf{x}, t) = \boldsymbol{\mu}(\mathbf{x}, t) - \frac{1}{2} \sigma^2(t) \nabla_{\mathbf{x}} \log p_t(\mathbf{x})\]于是,与原始 SDE 具有相同概率密度演化的确定性 ODE 为:
\[\frac{d\mathbf{x}}{dt} = \boldsymbol{\mu}(\mathbf{x}, t) - \frac{1}{2} \sigma^2(t) \nabla_{\mathbf{x}} \log p_t(\mathbf{x})\]条件生成与引导
在实际应用中,我们不仅想生成 $p(\mathbf{x})$,更想生成条件分布 $p(\mathbf{x}|\mathbf{c})$ (例如根据文本 $\mathbf{c}$ 生成图像)。
Classifier Guidance
利用贝叶斯公式,条件 Score 可以分解为: \(\nabla_\mathbf{x} \log p(\mathbf{x}|\mathbf{c}) = \nabla_\mathbf{x} \log p(\mathbf{x}) + \nabla_\mathbf{x} \log p(\mathbf{c}|\mathbf{x})\)
- $\nabla_\mathbf{x} \log p(\mathbf{x})$: 无条件 Score(由 Diffusion 模型提供)。
- $\nabla_\mathbf{x} \log p(\mathbf{c}|\mathbf{x})$: 分类器的梯度。它告诉我们“如何修改图片 $\mathbf{x}$,使其更像类别 $\mathbf{c}$”。
为了增强控制力,我们引入引导尺度 $\lambda$ (Guidance Scale):
\[\hat{s}_\theta(\mathbf{x}, \mathbf{c}) = \nabla_\mathbf{x} \log p(\mathbf{x}) + \lambda \nabla_\mathbf{x} \log p(\mathbf{c}|\mathbf{x})\]当 $\lambda > 1$ 时,生成过程会牺牲多样性以换取与条件 $\mathbf{c}$ 更高的匹配度。
Classifier-Free Guidance (CFG)
分类器引导需要额外训练一个抗噪分类器,成本高且复杂。CFG 提出用一个网络同时学习无条件和条件 Score。 训练时,以一定概率(如 10%~20%)将条件 $\mathbf{c}$ 置空(Null)作为无条件分布 $p(x)$。
在采样阶段,利用线性组合构造最终 Score:
\[\begin{aligned} \hat{s}_\theta(\mathbf{x}, \mathbf{c}) &= (1 + \lambda) \nabla_\mathbf{x} \log p(\mathbf{x}|\mathbf{c}) - \lambda \nabla_\mathbf{x} \log p(\mathbf{x}) \\ &= \nabla_\mathbf{x} \log p(\mathbf{x}|\mathbf{c}) + \lambda (\nabla_\mathbf{x} \log p(\mathbf{x}|\mathbf{c}) - \nabla_\mathbf{x} \log p(\mathbf{x})) \end{aligned}\]代码
VE-SDE + ODE 采样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll
# ==========================================
# 1. SDE 定义 (VE-SDE)
# ==========================================
def marginal_prob_std(t, sigma_min, sigma_max):
t = torch.as_tensor(t, device=device)
return sigma_min * (sigma_max / sigma_min) ** t
def diffusion_coeff(t, sigma_min, sigma_max):
t = torch.as_tensor(t, device=device)
sigma = marginal_prob_std(t, sigma_min, sigma_max)
return sigma * torch.sqrt(
torch.tensor(2 * (np.log(sigma_max) - np.log(sigma_min)), device=device)
)
# ==========================================
# 2. 模型定义 (ScoreNet)
# ==========================================
class GaussianFourierProjection(nn.Module):
def __init__(self, embed_dim, scale=1.5):
super().__init__()
self.W = nn.Parameter(torch.randn(embed_dim // 2) * scale, requires_grad=False)
def forward(self, x):
x_proj = x[:, None] * self.W[None, :] * 2 * np.pi
return torch.cat([torch.sin(x_proj), torch.cos(x_proj)], dim=-1)
class ScoreNet(nn.Module):
def __init__(self, sigma_min, sigma_max):
super().__init__()
self.sigma_min = sigma_min
self.sigma_max = sigma_max
self.embed = GaussianFourierProjection(64, scale=1.5)
self.net = nn.Sequential(
nn.Linear(64 + 2, 256),
nn.GELU(),
nn.Linear(256, 256),
nn.GELU(),
nn.Linear(256, 256),
nn.GELU(),
nn.Linear(256, 2),
)
def forward(self, x, t):
embed = self.embed(t)
h = torch.cat([x, embed], dim=-1)
output = self.net(h)
std = marginal_prob_std(t, self.sigma_min, self.sigma_max)
output = output / std[:, None]
return output
# ==========================================
# 3. 损失函数
# ==========================================
def loss_fn(model, x, sigma_min, sigma_max, eps=1e-5):
random_t = torch.rand(x.shape[0], device=x.device) * (1.0 - eps) + eps
z = torch.randn_like(x)
std = marginal_prob_std(random_t, sigma_min, sigma_max)
perturbed_x = x + z * std[:, None]
score = model(perturbed_x, random_t)
loss = torch.mean(torch.sum((score * std[:, None] + z) ** 2, dim=(1)))
return loss
# ==========================================
# 4. ODE 采样器 (最稳健)
# ==========================================
def ode_sampler(model, sigma_min, sigma_max, num_steps=1000, batch_size=1000):
model.eval()
device = next(model.parameters()).device
t = torch.ones(batch_size, device=device)
# 初始化噪声分布
init_x = (
torch.randn(batch_size, 2, device=device)
* marginal_prob_std(t, sigma_min, sigma_max)[:, None]
)
time_steps = torch.linspace(1.0, 1e-3, num_steps, device=device)
step_size = time_steps[0] - time_steps[1]
x = init_x
with torch.no_grad():
for time_step in time_steps:
batch_time_step = torch.ones(batch_size, device=device) * time_step
g = diffusion_coeff(batch_time_step, sigma_min, sigma_max)
score = model(x, batch_time_step)
# ODE update: dx = -0.5 * g^2 * score * dt
drift = 0.5 * (g[:, None] ** 2) * score * step_size
x = x + drift
return x
# ==========================================
# 5. 主程序
# ==========================================
if __name__ == "__main__":
device = "cuda" if torch.cuda.is_available() else "cpu"
print(f"Using device: {device}")
# 超参数
sigma_min = 0.01
sigma_max = 10.0
lr = 1e-3
n_epochs = 5000
batch_size = 1024
# 数据标准化
X_np, _ = make_swiss_roll(n_samples=3000, noise=0.5)
X_np = X_np[:, [0, 2]]
data_mean = np.mean(X_np, axis=0)
data_std = np.std(X_np, axis=0)
X_norm = (X_np - data_mean) / data_std
dataset = torch.tensor(X_norm, dtype=torch.float32).to(device)
score_model = ScoreNet(sigma_min, sigma_max).to(device)
optimizer = optim.Adam(score_model.parameters(), lr=lr)
print("training...")
loss_history = []
for epoch in range(n_epochs):
optimizer.zero_grad()
indices = torch.randint(0, dataset.shape[0], (batch_size,))
data_batch = dataset[indices]
loss = loss_fn(score_model, data_batch, sigma_min, sigma_max)
loss.backward()
optimizer.step()
loss_history.append(loss.item())
if epoch % 500 == 0 or epoch == n_epochs - 1:
print(f"Epoch {epoch} | Loss: {loss.item():.4f}")
print("生成样本中...")
generated_samples = ode_sampler(score_model, sigma_min, sigma_max)
generated_samples = generated_samples.cpu().numpy()
# 反归一化以便在原始尺度上绘图
generated_samples_restored = generated_samples * data_std + data_mean
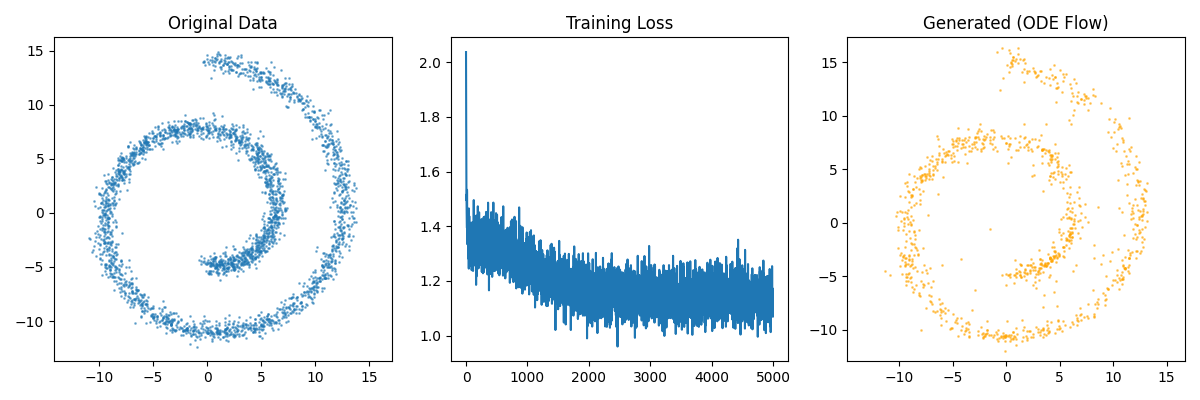
# 可视化
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.scatter(X_np[:, 0], X_np[:, 1], s=1, alpha=0.5)
plt.title("Original Data")
plt.axis("equal")
plt.subplot(1, 3, 2)
plt.plot(loss_history)
plt.title("Training Loss")
plt.ylim()
plt.subplot(1, 3, 3)
plt.scatter(
generated_samples_restored[:, 0],
generated_samples_restored[:, 1],
s=1, c="orange", alpha=0.5
)
plt.title("Generated (ODE Flow)")
plt.axis("equal")
plt.tight_layout()
plt.show()