博弈论笔记

发表于 2025/11/22 更新于 2025/11/23

作者 gctoph

91 分钟阅读

博弈论笔记

信任的演化（The Evolution of Trust）

长期关系 - 凝聚性社会资本

善良原则: 首先展示合作的善意;
正义原则: 每回合对方如何对待你, 下一回合你就如何对待对方;
宽容原则: 在有环境噪声(误解)的情况下, 即使结果是糟糕的, 但若不能确定对方动机欺骗, 表现出信任和宽容。

在小世界网络中的结论

对于静态小世界网络，若捷径数量较少，原则仍然是：善良、正义、宽容
对于静态小世界网络，若捷径数量较多，原则是欺骗

实际实验：对于静态小世界网络，无论捷径数量多少，都因为从众效应取决于第一个人一开始的行为

若可以自由选择和谁交往，更容易建立合作。
做出选择本身就很有力量

最后通牒博弈（Ultimatum Game）

最后通牒博弈是行为经济学中的经典实验：

一人（Proposer）被给予一笔固定金额（如10元），决定如何分配给自己和对方；
另一人（Responder）可选择接受或拒绝该分配；
若接受，双方按方案获得金钱；若拒绝，双方都一无所获。

传统观点：Proposer 应只给对方1元（因 Responder 作为理性人应接受任何正收益），但现实中人们常拒绝不公平分配，表现出公平偏好与惩罚意愿。

棋盘

生态系统

Proposer：每次分配10元，自留 x 元（x ∈ {1,2,…,9}），给予对方 (10−x) 元。
Responder：设定最低接受额 y 元（y ∈ {1,2,…,9}），仅当收到 ≥ y 时才接受。

互动合作是生存基础：没有对方，个体无法获得金钱或完成交易。

机会均等

所有个体起始 生命值(机会数) = 100，金钱 = 0；
每次互动（无论成功与否）消耗1点生命值；
生命值归零 → 退出本轮游戏。

自由选择

每轮从所有存活个体中随机配对，无人优先、无人被排除；

若 $10−x \geq y$：合作成功 → 最多连续交易10次（或至某方生命耗尽）；
否则：合作失败 → 双方无收入。双方不会长期绑定，立刻参与下一轮随机配对；

代际演化（自然选择, 适者生存）

每代结束后：

按总赚钱数衡量适应度；
群体规模恒定：各角色1000人，共2000个体。
分别淘汰最穷的30人；
分别根据金钱作为权重随机抽取复制30人的策略（x 或 y）, 新一代重置生命值=100，金钱=0；
在复制产生后代时，有5%概率突变，随机改变策略（x 或 y）。
演化100代。

求解

Evolutionarily Stable Strategy，ESS

纳什均衡的特例：当种群采用了一种对策后，其他策略在自然选择的压力下都无法侵入这个种群。

代码

  
# pip install matplotlib

import random
import matplotlib.pyplot as plt

# ================= 全局配置 =================
NUM_AGENTS = 1000       # 每种角色的数量
INITIAL_HP = 100        # 初始生命值
ROUNDS_PER_SUCCESS = 10 # 合作成功后交易次数
TOTAL_GENERATIONS = 100 # 模拟多少代
NUM_ELIMINATED = 30     # 每代淘汰人数
MUTATION_RATE = 0.05    # 突变概率 (5%)


class Proposer:
    def __init__(self, id, x=None):
        self.id = id
        # x: 自留金额 (1-9), 留下的越多，给对方的(10-x)越少
        self.x = x if x is not None else random.randint(1, 9)
        self.hp = INITIAL_HP
        self.money = 0

    def reset_status(self):
        self.hp = INITIAL_HP
        self.money = 0
        
    def mutate(self):
        self.x = random.randint(1, 9)


class Responder:
    def __init__(self, id, y=None):
        self.id = id
        # y: 最低接受金额 (1-9)
        self.y = y if y is not None else random.randint(1, 9)
        self.hp = INITIAL_HP
        self.money = 0

    def reset_status(self):
        self.hp = INITIAL_HP
        self.money = 0

    def mutate(self):
        self.y = random.randint(1, 9)


def run_market_session(proposers, responders):
    """
    运行一代的市场互动，直到生命耗尽
    """
    while True:
        # 筛选活着的个体
        active_proposers = [a for a in proposers if a.hp > 0]
        active_responders = [p for p in responders if p.hp > 0]

        if not active_proposers or not active_responders:
            break

        # 随机配对
        random.shuffle(active_proposers)
        random.shuffle(active_responders)

        num_pairs = min(len(active_proposers), len(active_responders))

        for i in range(num_pairs):
            proposer = active_proposers[i]
            responder = active_responders[i]

            offer_to_responder = 10 - proposer.x
            min_accept = responder.y

            if offer_to_responder >= min_accept:
                # 合作成功：消耗生命，获得金钱
                # 交易次数受限于双方剩余生命值和最大交易上限
                rounds = min(ROUNDS_PER_SUCCESS, proposer.hp, responder.hp)
                
                gain_p = proposer.x * rounds
                gain_r = offer_to_responder * rounds
                
                proposer.money += gain_p
                responder.money += gain_r
                
                proposer.hp -= rounds
                responder.hp -= rounds
            else:
                # 合作失败：仅消耗1点生命，无金钱
                proposer.hp -= 1
                responder.hp -= 1


def evolve_population(agents, role_name):
    """
    演化逻辑：
    1. 淘汰最穷的 N 个。
    2. 从幸存者中，根据金钱权重随机选择父母来补充空缺。
    3. 新生儿有概率发生突变。
    """
    # 按金钱从高到低排序
    agents.sort(key=lambda agent: agent.money, reverse=True)

    # 1. 幸存者 (保留除了被淘汰者之外的所有人)
    survivors = agents[: NUM_AGENTS - NUM_ELIMINATED]
    
    # 繁殖权重
    weights = [a.money + 1e-6 for a in survivors]

    new_agents = []
    current_id_max = max(a.id for a in agents)

    # 2. 概率选择父母 (Roulette Wheel Selection)
    # random.choices 可以根据权重有放回地抽取
    parents = random.choices(survivors, weights=weights, k=NUM_ELIMINATED)

    for i, parent in enumerate(parents):
        new_id = current_id_max + i + 1
        
        # 繁殖
        if role_name == "Proposer":
            child = Proposer(new_id, x=parent.x)
        else:
            child = Responder(new_id, y=parent.y)
        
        # 3. 突变 (Mutation)
        if random.random() < MUTATION_RATE:
            child.mutate()
            
        new_agents.append(child)

    # 新一代
    next_generation = survivors + new_agents

    # 重置状态 (血量满，金钱清零)
    for agent in next_generation:
        agent.reset_status()

    return next_generation


def plot_evolution(history, title, filename, legend_labels):
    """
    绘制堆叠面积图
    """
    generations = range(len(history))
    strategies = range(1, 10)
    
    y_stack = []
    for s in strategies:
        counts = [gen_data.get(s, 0) for gen_data in history]
        y_stack.append(counts)

    plt.figure(figsize=(12, 6))
    
    # 使用 tab10 颜色盘
    cmap = plt.get_cmap('tab10')
    colors = [cmap(i) for i in range(9)]
    
    plt.stackplot(generations, y_stack, labels=legend_labels, colors=colors, alpha=0.85)
    
    plt.title(title, fontsize=14)
    plt.xlabel("Generation", fontsize=12)
    plt.ylabel("Number of Agents", fontsize=12)
    plt.xlim(0, len(history)-1)
    plt.ylim(0, NUM_AGENTS)
    
    plt.legend(loc='upper left', bbox_to_anchor=(1, 1), title="Strategy Value")
    plt.tight_layout()
    
    print(f"Saving plot: {filename} ...")
    plt.savefig(filename)
    plt.close()


def main():
    print(f"初始化模拟: {NUM_AGENTS} 个体, 突变率 {MUTATION_RATE}, 概率选择繁殖...")
    
    proposers = [Proposer(i) for i in range(NUM_AGENTS)]
    responders = [Responder(i) for i in range(NUM_AGENTS)]

    proposer_history = []
    responder_history = []

    # 记录第0代
    def record_history(agent_list, is_proposer=True):
        counts = {k: 0 for k in range(1, 10)}
        for a in agent_list:
            val = a.x if is_proposer else a.y
            counts[val] = counts.get(val, 0) + 1
        return counts

    proposer_history.append(record_history(proposers, True))
    responder_history.append(record_history(responders, False))

    for gen in range(1, TOTAL_GENERATIONS + 1):
        # 市场交易
        run_market_session(proposers, responders)

        # 演化
        proposers = evolve_population(proposers, "Proposer")
        responders = evolve_population(responders, "Responder")

        # 记录数据
        proposer_history.append(record_history(proposers, True))
        responder_history.append(record_history(responders, False))

        if gen % 20 == 0:
            print(f"Generation {gen} completed.")

    # === 绘图 ===
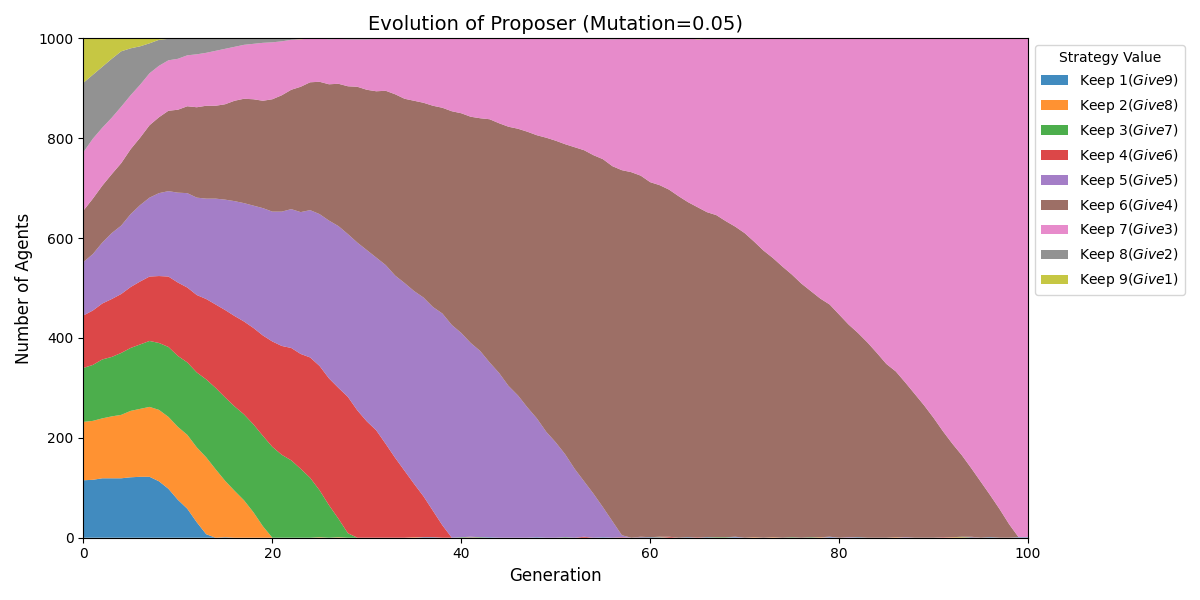
    p_labels = [f"Keep ${i} (Give ${10-i})" for i in range(1, 10)]
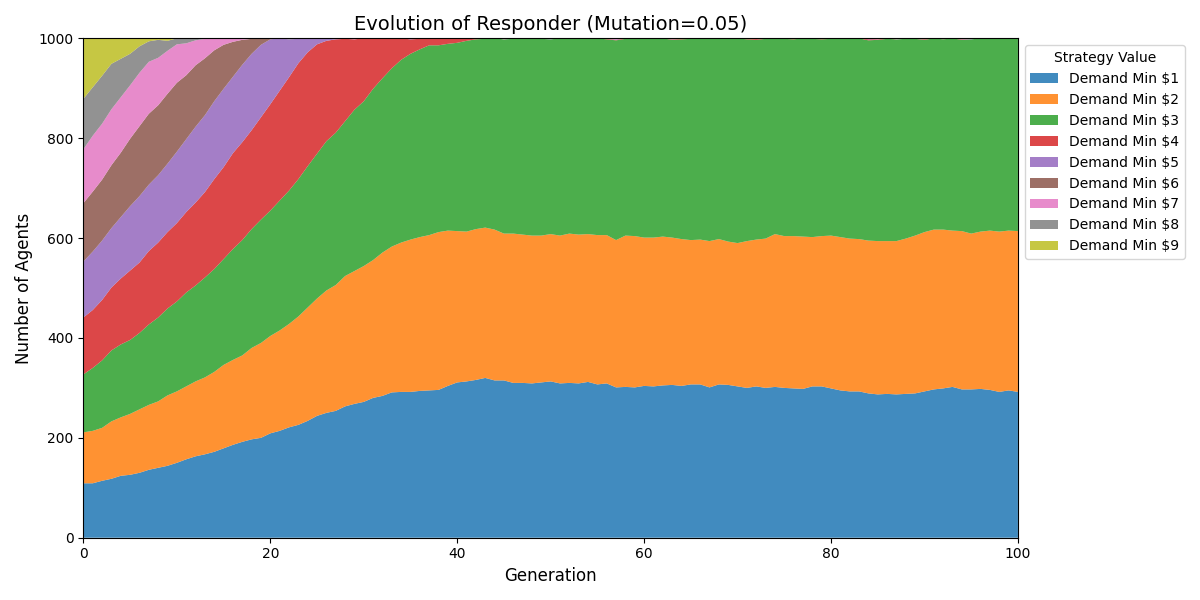
    r_labels = [f"Demand Min ${i}" for i in range(1, 10)]

    plot_evolution(
        proposer_history, 
        title=f"Evolution of Proposer (Mutation={MUTATION_RATE})", 
        filename="proposer_evolution_mut.png",
        legend_labels=p_labels
    )

    plot_evolution(
        responder_history, 
        title=f"Evolution of Responder (Mutation={MUTATION_RATE})", 
        filename="responder_evolution_mut.png",
        legend_labels=r_labels
    )

    # === 打印最终统计 ===
    print("\n=== 最终结果 ===")
    
    print("\nProposer 分布 (x = 自己保留):")
    final_p = proposer_history[-1]
    sorted_p = sorted(final_p.items(), key=lambda item: item[1], reverse=True)
    for x, count in sorted_p:
        if count > 0:
            print(f"  自留 ${x} (给对方 ${10-x}): {count} 人")

    print("\nResponder 分布 (y = 最低接受):")
    final_r = responder_history[-1]
    sorted_r = sorted(final_r.items(), key=lambda item: item[1], reverse=True)
    for y, count in sorted_r:
        if count > 0:
            print(f"  要求 ${y}: {count} 人")

if __name__ == "__main__":
    main()

运行结果

Proposer 分布 (x = 自己保留):
  自留 $7 (给对方 $3): 999 人
  自留 $1 (给对方 $9): 1 人

Responder 分布 (y = 最低接受):
  要求 $3: 385 人
  要求 $2: 322 人
  要求 $1: 292 人
  要求 $6: 1 人

结论：中期六四分成；长期七三分成。

主要看Proposer分布，尽管有些Responder底线是要求1元，实际每次合作也是获得3元。

其他初始分布

正态分布参数：

策略空间是 $1$ 到 $9$。
均值 ($\mu$)：设为 $5$ (中间值)。
标准差 ($\sigma$)：设为 $2$。根据 $3\sigma$ 原则，$5 \pm 6$ 覆盖了绝大多数情况，裁剪后能形成一个很好的中间高、两边低的钟形曲线。

  
# 正态分布配置
INIT_MU = 5     # 均值
INIT_SIGMA = 2  # 标准差

def get_truncated_normal(mu=5, sigma=2, low=1, high=9):
    """
    生成截断的正态分布整数：
    1. 生成高斯分布浮点数
    2. 四舍五入取整
    3. 裁剪到 [low, high] 区间
    """
    val = random.gauss(mu, sigma)
    val = round(val)
    if val < low:
        return low
    if val > high:
        return high
    return int(val)

  
        self.x = x if x is not None else get_truncated_normal(INIT_MU, INIT_SIGMA, 1, 9)
        self.y = y if y is not None else get_truncated_normal(INIT_MU, INIT_SIGMA, 1, 9)

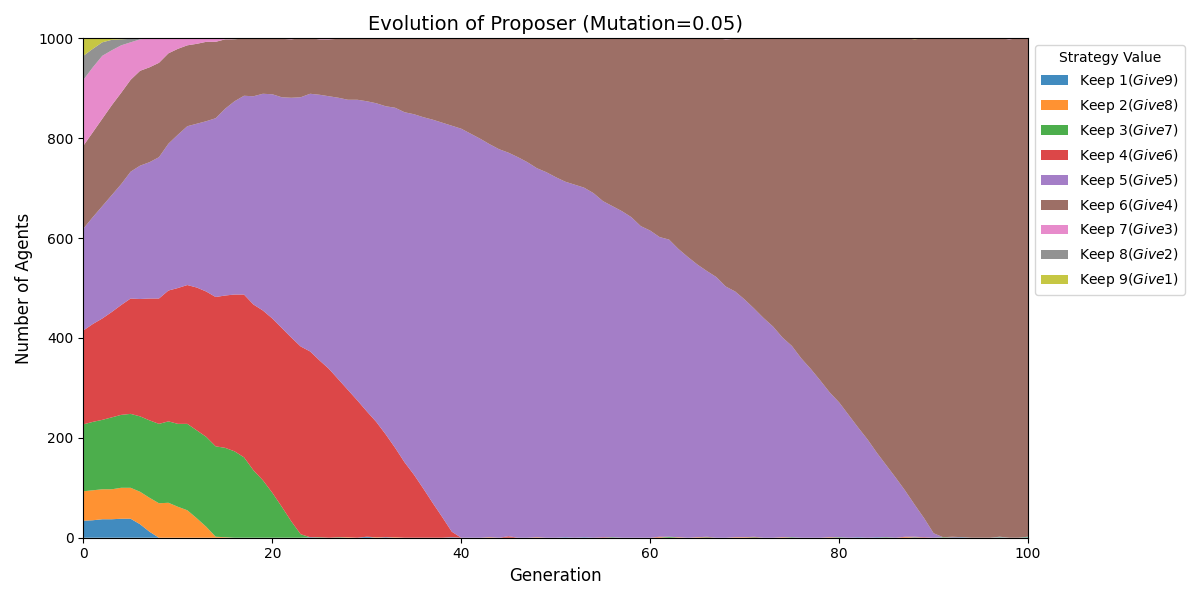
Proposer 分布 (x = 自己保留):
  自留 $6 (给对方 $4): 997 人
  自留 $1 (给对方 $9): 1 人
  自留 $3 (给对方 $7): 1 人
  自留 $9 (给对方 $1): 1 人

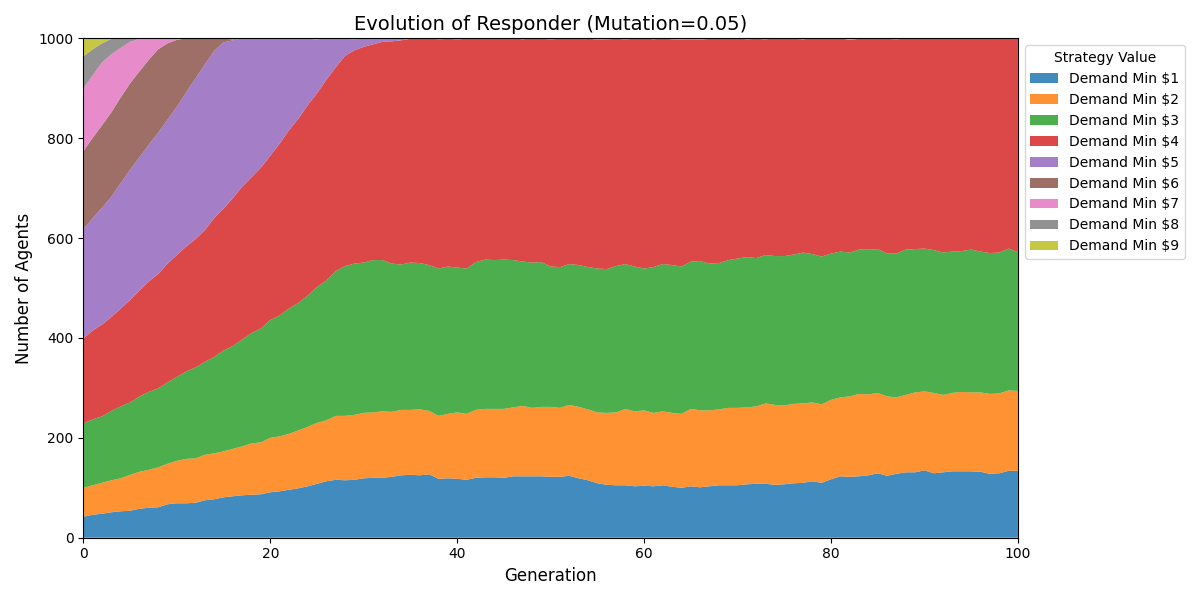
Responder 分布 (y = 最低接受):
  要求 $4: 427 人
  要求 $3: 278 人
  要求 $2: 160 人
  要求 $1: 134 人
  要求 $6: 1 人

结论：若初始分布并非均匀，最终可能会完全收敛到六四分成。

主要看Proposer分布，尽管有些Responder底线是要求1元，实际每次合作也是获得4元。

蜈蚣博弈 (Centipede Game)

规则：
- A 和 B 轮流做决定。桌上有两堆钱，起初很少（比如 A:4, B:1）。
- 轮到谁，谁就有两个选择：
  1. 拿走（Take）：拿走较多的一堆，游戏结束，对方拿较少的一堆。
  2. 推进（Push）：把钱推给对方，此时总金额增加，两堆钱的数量翻转并增长。
- 游戏持续 100 轮。如果走到最后，两人都能拿到极高的金额（比如几百万）。
SPNE（子博弈精炼纳什均衡）解：
- 在第 100 轮，也就是最后一轮，最后那个人为了利益最大化，一定会选择“拿走”。
- 既然第 100 轮必被“拿走”，第 99 轮的人为了不吃亏，也会选择“拿走”。
- 倒推回第 1 轮：A 应该立刻结束游戏，拿走 4 元，B 拿走 1 元。

棋盘

规则设定

配对：随机抽取两人，随机分配 Player A (先手) 和 Player B (后手)。
回合：共 100 个节点（回合）。
决策：轮到的一方可以选择 “拿走 (Take)” 或 “推进 (Push)”。
- A 在奇数回合决策 (1, 3, 5…)
- B 在偶数回合决策 (2, 4, 6…)
收益结构：
- 每一轮只要“推进”，奖池总额就会增加。
- 背叛诱惑：在任何一轮 $t$，如果当前行动者选择“拿走”，他获得的收益大于 “如果他推进，而对手在下一轮 $t+1$ 拿走”时他能获得的收益。
- 公式：
  - 若在第 $t$ 轮结束：
  - 拿走者 (Taker) 获得：$t + 2$
  - 被动者 (Loser) 获得：$t - 1$
  - 验证纳什均衡：假设我在第 $99$ 轮。拿走得 $101$。若推进，对手在 $100$ 轮拿走，我得 $99$。因为 $101 > 99$，所以我必须在 $99$ 轮拿走。以此类推，直到第1轮。
- 天国BONUS：若玩家信任到最后，均会获得额外奖励。

策略 (基因)

每个个体拥有一个基因 stop_threshold (1 到 101)：

代表个体的信任边界或贪婪程度。
含义：“只要轮到我，且当前回合数 $\ge$ 我的 stop_threshold，我就拿走钱；否则我推进。”
若值为 101，代表永远合作（Always Cooperate）。
若值为 1，代表极其自私/理性，第一轮就拿。

代码

  
import random
import matplotlib.pyplot as plt
import numpy as np

# ================= 全局配置 =================
NUM_AGENTS = 1000         # 个体数量
TOTAL_GENERATIONS = 10000 # 模拟代数
NUM_ELIMINATED = 100      # 每代淘汰数
MUTATION_RATE = 0.05      # 突变率
MUTATION_STRENGTH = 10    # 突变时策略波动的幅度
MAX_ROUNDS = 100          # 蜈蚣博弈最大回合数
BONUS = False

class Agent:
    def __init__(self, id, strategy=None):
        self.id = id
        # strategy: 计划在哪一回合(及以后)背叛。
        if strategy is not None:
            self.strategy = strategy
        else:
            self.strategy = random.randint(1, MAX_ROUNDS + 1)
            
        self.money = 0

    def reset_status(self):
        self.money = 0
        
    def mutate(self):
        # 突变：在原有策略附近波动，或者小概率完全重置
        if random.random() < 0.2:
            self.strategy = random.randint(1, MAX_ROUNDS + 1)
        else:
            change = random.randint(-MUTATION_STRENGTH, MUTATION_STRENGTH)
            self.strategy += change
            self.strategy = max(1, min(MAX_ROUNDS + 1, self.strategy))

def play_centipede(p1, p2):
    """
    进行一次蜈蚣博弈
    P1 在奇数轮行动 (1, 3, 5...)
    P2 在偶数轮行动 (2, 4, 6...)
    """
    
    current_round = 1
    payoff_p1 = 0
    payoff_p2 = 0
    
    # 游戏主循环
    while current_round <= MAX_ROUNDS:
        is_p1_turn = (current_round % 2 != 0)
        
        active_player = p1 if is_p1_turn else p2
        
        # 如果当前回合 >= 心理防线，就会拿走钱
        if current_round >= active_player.strategy:
            # === 背叛 (Take) ===
            # Taker: round + 2; Loser: round - 1
            payoff_taker = current_round + 2
            payoff_loser = max(0, current_round - 1)
            
            if is_p1_turn:
                payoff_p1 = payoff_taker
                payoff_p2 = payoff_loser
            else:
                payoff_p2 = payoff_taker
                payoff_p1 = payoff_loser
                
            break
        
        if current_round == MAX_ROUNDS and BONUS:
            # 合作通关奖励：比如每人 120
            payoff_p1 = payoff_p2 = MAX_ROUNDS + 20
            break
        
        # === 推进 (Push) ===
        current_round += 1

    p1.money += payoff_p1
    p2.money += payoff_p2

def evolve_population(agents):
    # 排序：钱多的在前
    agents.sort(key=lambda a: a.money, reverse=True)
    # 淘汰最穷的
    survivors = agents[: NUM_AGENTS - NUM_ELIMINATED]
    # 繁殖：基于财富权重的轮盘赌
    # 为了防止负数或0导致错误，加一个小底数
    weights = [max(0, a.money) + 1 for a in survivors]
    
    parents = random.choices(survivors, weights=weights, k=NUM_ELIMINATED)
    
    new_agents = []
    max_id = max(a.id for a in agents)
    
    for i, parent in enumerate(parents):
        child = Agent(max_id + i + 1, strategy=parent.strategy)
        if random.random() < MUTATION_RATE:
            child.mutate()
        new_agents.append(child)
        
    next_gen = survivors + new_agents
    for a in next_gen:
        a.reset_status()
        
    return next_gen

def main():
    agents = [Agent(i) for i in range(NUM_AGENTS)]
    
    # 记录每一代所有人的策略，用于画热力图
    # 形状: [Generation][Strategy_Bin]
    history_distribution = []

    print("开始蜈蚣博弈演化模拟...")

    for gen in range(TOTAL_GENERATIONS):
        # 随机配对
        random.shuffle(agents)
        # 两两对战
        for i in range(0, len(agents), 2):
            if i+1 < len(agents):
                play_centipede(agents[i], agents[i+1])
        
        # 记录统计
        strategies = [a.strategy for a in agents]
        # 将策略分桶 (Bins)，比如每5个回合一个桶，或者直接按1-101记录
        # 这里直接记录 1-101 的频率
        counts = [0] * (MAX_ROUNDS + 2)
        for s in strategies:
            idx = min(s, MAX_ROUNDS + 1)
            counts[idx] += 1
        history_distribution.append(counts)
        
        avg_strat = sum(strategies) / len(strategies)
        if gen % 50 == 0 or gen == TOTAL_GENERATIONS - 1:
            print(f"Gen {gen}: Avg Strategy Threshold = {avg_strat:.2f} (Higher = More Trust)")

        # 演化
        agents = evolve_population(agents)

    # === 绘图 ===
    # 转换数据用于热力图: 行=策略值(1-100+), 列=代数
    data_matrix = np.array(history_distribution).T # 转置：Y轴是策略，X轴是时间
    # 去掉索引0 (没用到)
    data_matrix = data_matrix[1:, :]
    
    plt.figure(figsize=(12, 8))
    
    # 使用 LogNorm 可能能更好地显示低频但关键的突变，但线性通常足够
    plt.imshow(data_matrix, aspect='auto', cmap='inferno', origin='lower', 
               extent=[0, TOTAL_GENERATIONS, 1, MAX_ROUNDS+1])
    
    plt.colorbar(label='Number of Agents')
    plt.title('Evolution of Trust in Centipede Game\n(Y=Round they plan to defect, X=Generation)', fontsize=14)
    plt.xlabel('Generation')
    plt.ylabel('Strategy (Stop Threshold)')
    
    # 标注区域意义
    plt.text(TOTAL_GENERATIONS*0.05, 5, 'Rational/Selfish (Nash)', color='white', fontsize=12, fontweight='bold')
    plt.text(TOTAL_GENERATIONS*0.05, 95, 'Cooperative/Trusting', color='white', fontsize=12, fontweight='bold')

    filename = "centipede_heatmap.png"
    print(f"Saving heatmap to {filename}...")
    plt.savefig(filename)
    plt.close()

if __name__ == "__main__":
    main()

运行结果

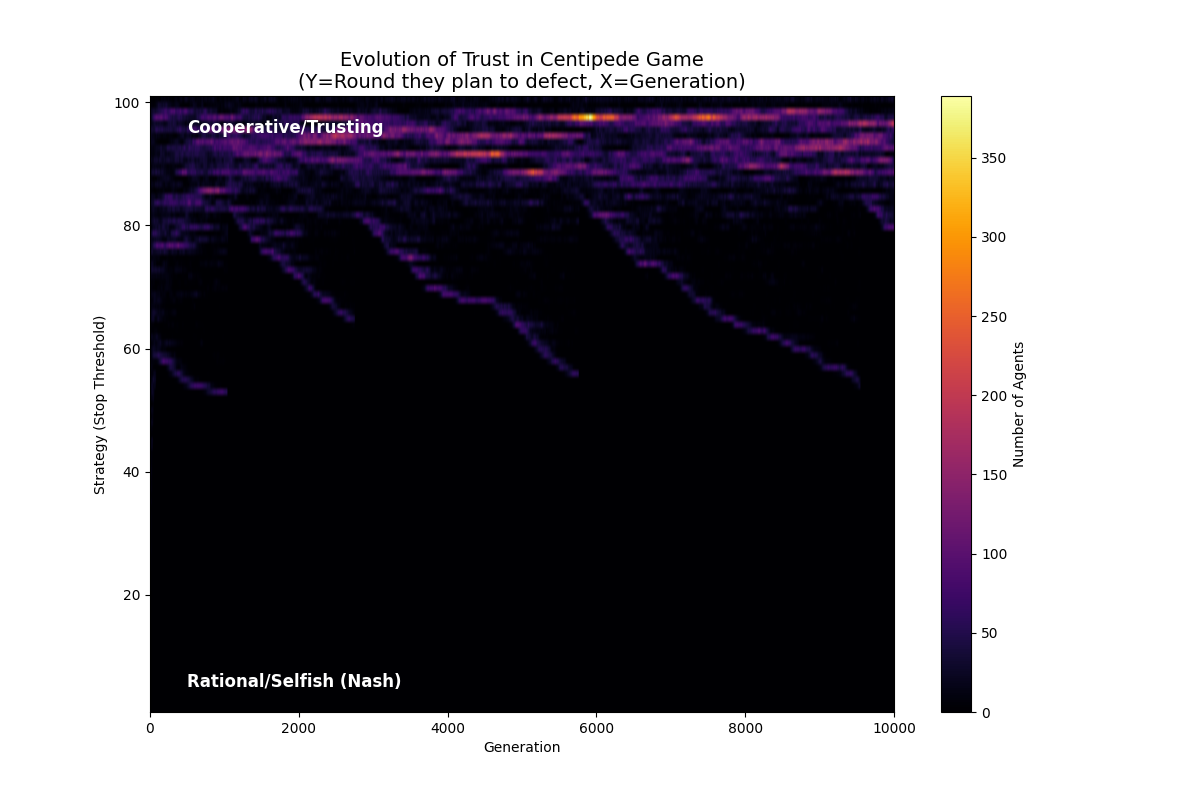
低生存压力

NUM_AGENTS = 1000         # 个体数量
TOTAL_GENERATIONS = 10000 # 模拟代数
NUM_ELIMINATED = 50       # 每代淘汰数
BONUS = False

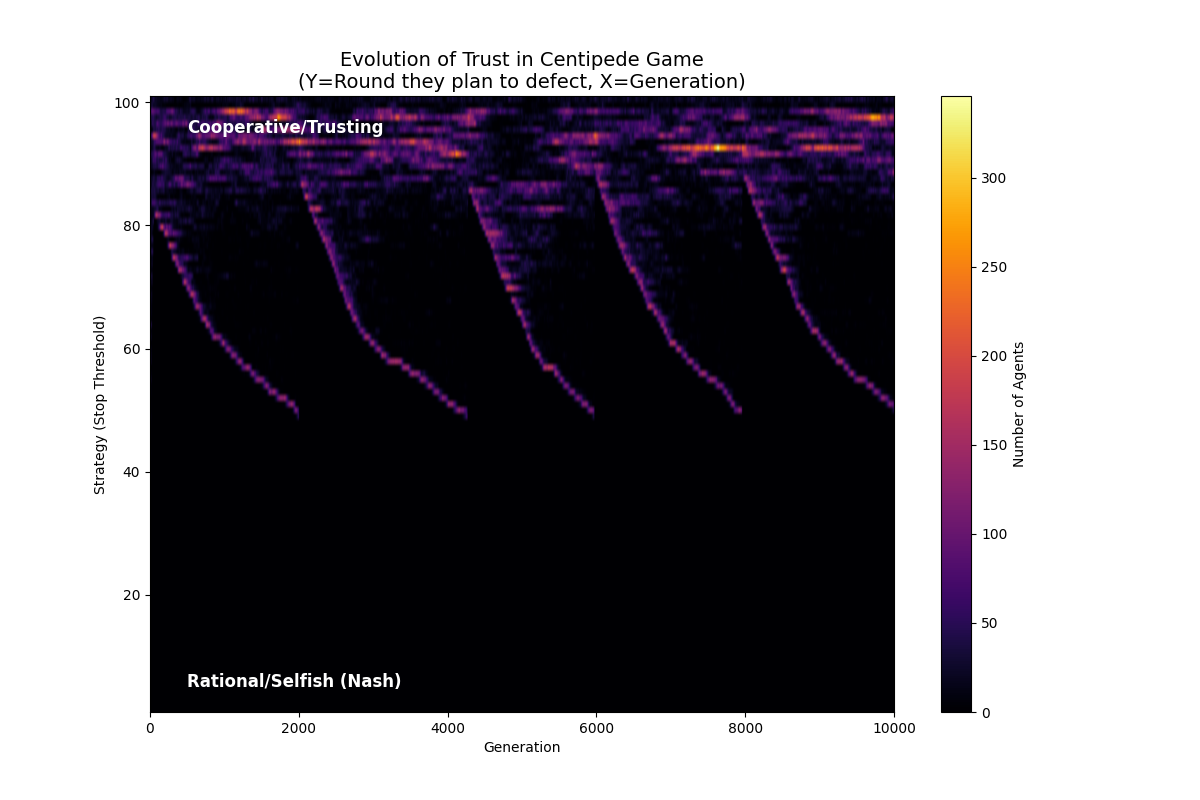
中生存压力

NUM_ELIMINATED = 100       # 每代淘汰数

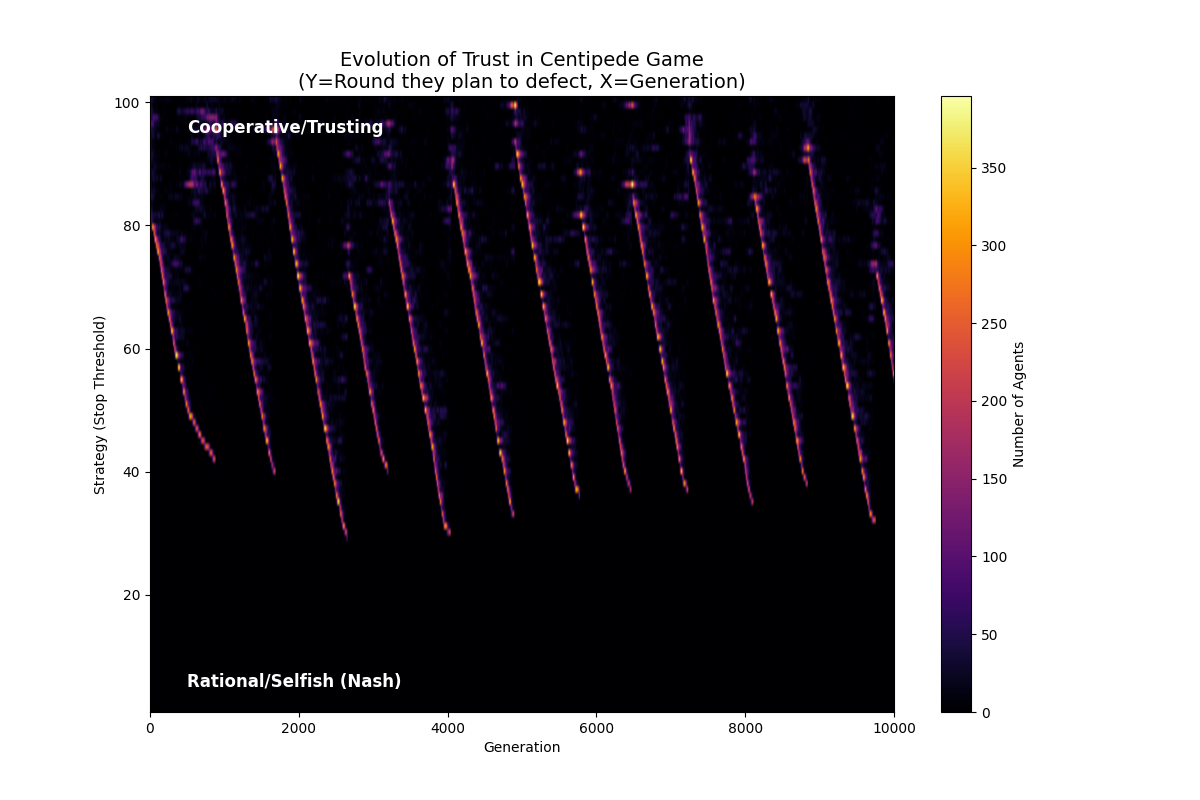
高生存压力

NUM_ELIMINATED = 200       # 每代淘汰数

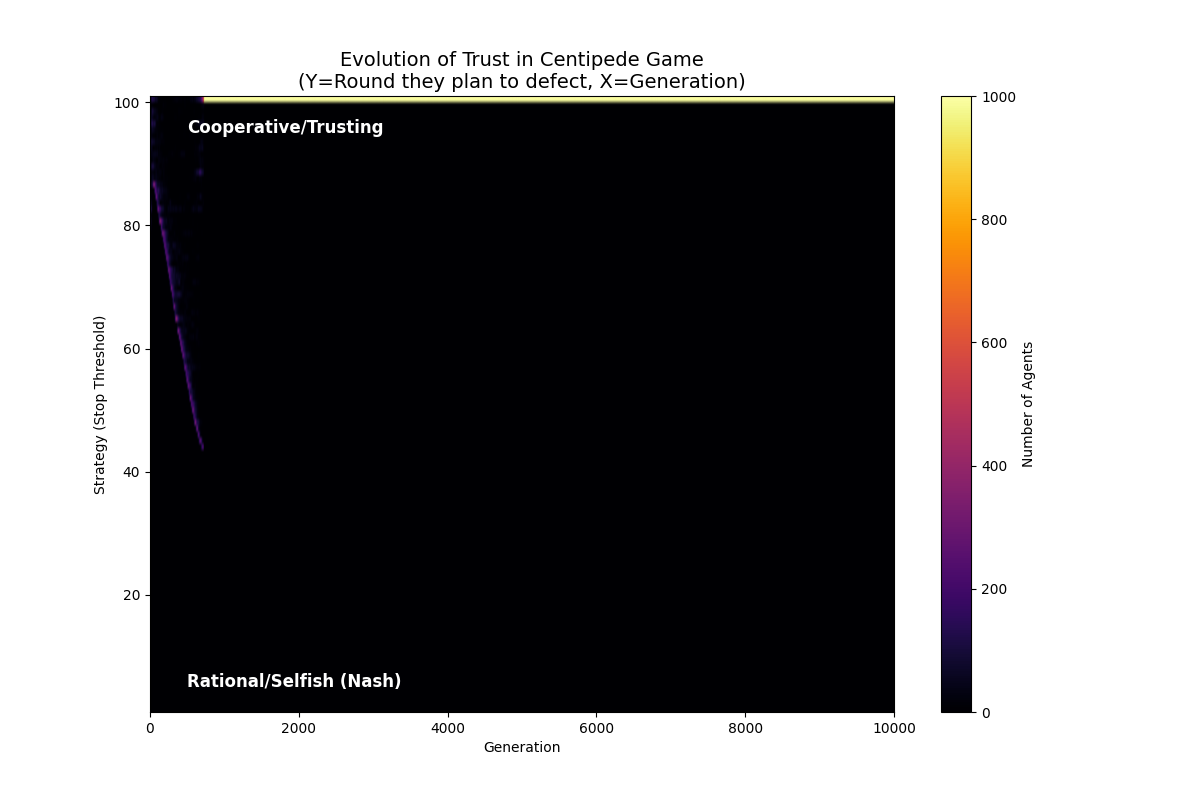
高生存压力+bonus

NUM_ELIMINATED = 200       # 每代淘汰数
BONUS = True

结论

蜈蚣博弈常出现循环：合作建立 -> 背叛者收割 -> 信任崩塌 -> 重新建立
一旦进入BONUS区域，可以跳出诅咒循环

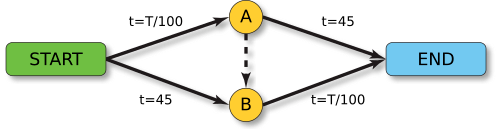
布雷斯悖论 (Braess’s Paradox)

设定通勤人数 $N = 4000$。

起点 S -> 终点 E。
路径 0 (上路)：$S \to A \to E$。
- $S \to A$：拥堵路段，耗时 $= \text{流量} / 100$。
- $A \to E$：宽阔公路，耗时 $= 45$ (固定)。
路径 1 (下路)：$S \to B \to E$。
- $S \to B$：宽阔公路，耗时 $= 45$ (固定)。
- $B \to E$：拥堵路段，耗时 $= \text{流量} / 100$。
路径 2 (捷径)：$S \to A \to B \to E$。
- $A \to B$：耗时 $= 0$ (超极速)。
- 关键：结合了上路的第一段和下路的第二段。

阶段一：只有原有道路（Path A 和 Path B）。系统会自动达到 50/50 的平衡。
阶段二：第 30 代时，政府修好了捷径。群体模仿更快的路线，蜂拥而至，最终导致整体崩溃。

代码

  
import random
import matplotlib.pyplot as plt
import numpy as np

# ================= 全局配置 =================
NUM_AGENTS = 4000         # 司机数量
TOTAL_GENERATIONS = 100   # 模拟总代数
ROAD_OPEN_GEN = 30        # 第30代修好捷径
MUTATION_RATE = 0.05      # 司机尝试换路的概率
NUM_ELIMINATED = 500      # 每代选择模仿捷径司机的数量

# 道路参数
FIXED_TIME = 45           # 宽阔公路的固定时间
CAPACITY_FACTOR = 100     # 拥堵系数 (流量/100)

class Agent:
    def __init__(self, id, path=None):
        self.id = id
        # path: 0=Top(S-A-E), 1=Bottom(S-B-E), 2=Shortcut(S-A-B-E)
        if path is not None:
            self.path = path
        else:
            # 初始状态只有 0 和 1，没有捷径
            self.path = random.choice([0, 1])
        
        self.commute_time = 0

def calculate_traffic_times(agents):
    # 1. 统计各路径人数
    counts = {0: 0, 1: 0, 2: 0}
    for a in agents:
        counts[a.path] += 1
        
    # 2. 计算各路段流量
    # N0走 S->A->E
    # N1走 S->B->E
    # N2走 S->A->B->E
    n0 = counts[0]
    n1 = counts[1]
    n2 = counts[2]
    
    flow_SA = n0 + n2  # 上路第一段
    flow_BE = n1 + n2  # 下路第二段
    
    # 3. 计算各路段时间
    time_SA = flow_SA / CAPACITY_FACTOR
    time_SB = FIXED_TIME
    time_AE = FIXED_TIME
    time_BE = flow_BE / CAPACITY_FACTOR
    time_AB = 0
    
    # 4. 计算总路径耗时
    cost_path_0 = time_SA + time_AE
    cost_path_1 = time_SB + time_BE
    cost_path_2 = time_SA + time_AB + time_BE
    
    path_costs = {
        0: cost_path_0,
        1: cost_path_1,
        2: cost_path_2
    }
    
    # 将时间赋值给每个个体
    for a in agents:
        a.commute_time = path_costs[a.path]
        
    return path_costs, counts

def evolve_population(agents, shortcut_open):
    # 排序：时间短（Commute Time 小）的排前面
    agents.sort(key=lambda a: a.commute_time)
    
    # 表现最差的人（通勤时间最长）会被淘汰，并模仿表现好的人
    survivors = agents[: NUM_AGENTS - NUM_ELIMINATED]
    
    # 简单的模仿机制：完全随机从幸存者中挑选父母
    new_agents = []
    max_id = max(a.id for a in agents)
    
    for i in range(NUM_ELIMINATED):
        parent = random.choice(survivors)
        # 继承父母的路线
        child_path = parent.path
        
        # 突变：尝试探索其他路线
        if random.random() < MUTATION_RATE:
            options = [0, 1, 2] if shortcut_open else [0, 1]
            child_path = random.choice(options)
            
        new_agents.append(Agent(max_id + i + 1, path=child_path))
        
    return survivors + new_agents

def main():
    agents = [Agent(i) for i in range(NUM_AGENTS)]
    
    history_avg_time = []
    history_counts = {0: [], 1: [], 2: []}

    print("开始布雷斯悖论交通模拟...")

    for gen in range(TOTAL_GENERATIONS):
        shortcut_open = (gen >= ROAD_OPEN_GEN)
        
        # 如果捷径没开，强制所有选路2的人重置回0或1 (处理边界情况)
        if not shortcut_open:
            for a in agents:
                if a.path == 2:
                    a.path = random.choice([0, 1])

        # 1. 计算时间
        costs, counts = calculate_traffic_times(agents)
        
        # 统计平均时间
        total_time = sum(a.commute_time for a in agents)
        avg_time = total_time / NUM_AGENTS
        history_avg_time.append(avg_time)
        
        history_counts[0].append(counts[0])
        history_counts[1].append(counts[1])
        history_counts[2].append(counts[2])
        
        if gen % 10 == 0 or gen == ROAD_OPEN_GEN:
            status = " [SHORTCUT OPEN]" if shortcut_open else ""
            print(f"Gen {gen}{status}: Avg Time = {avg_time:.2f} min. "
                  f"(Path Costs: T0={costs[0]:.1f}, T1={costs[1]:.1f}, T2={costs[2]:.1f})")

        # 2. 演化
        agents = evolve_population(agents, shortcut_open)

    # === 绘图 ===
    gens = range(TOTAL_GENERATIONS)
    
    fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 10), sharex=True)
    
    # 图1：平均通勤时间
    ax1.plot(gens, history_avg_time, color='red', linewidth=3, label='Average Commute Time')
    ax1.axvline(x=ROAD_OPEN_GEN, color='black', linestyle='--', label='Shortcut Opened')
    ax1.set_ylabel('Time (Minutes)')
    ax1.set_title("Braess's Paradox: Why New Roads Make Traffic Worse")
    ax1.legend()
    ax1.grid(True, alpha=0.3)
    
    # 标注文本
    start_time = history_avg_time[5]
    end_time = history_avg_time[-1]
    ax1.text(5, start_time + 2, f"Nash Equilibrium 1\nTime ~ {start_time:.0f} min", color='blue')
    ax1.text(TOTAL_GENERATIONS - 30, end_time - 5, f"Nash Equilibrium 2\nTime ~ {end_time:.0f} min", color='red')

    # 图2：各路线人数堆叠图
    y = np.vstack([history_counts[0], history_counts[1], history_counts[2]])
    ax2.stackplot(gens, y, labels=['Path Top (S-A-E)', 'Path Bottom (S-B-E)', 'Path Shortcut (S-A-B-E)'], 
                  colors=['#1f77b4', '#ff7f0e', '#2ca02c'], alpha=0.8)
    ax2.axvline(x=ROAD_OPEN_GEN, color='black', linestyle='--')
    ax2.set_xlabel('Generation')
    ax2.set_ylabel('Number of Drivers')
    ax2.set_title('Traffic Distribution')
    ax2.legend(loc='lower right')
    
    plt.tight_layout()
    filename = "braess_paradox_simulation.png"
    print(f"Saving plot to {filename}...")
    plt.savefig(filename)
    plt.show()

if __name__ == "__main__":
    main()

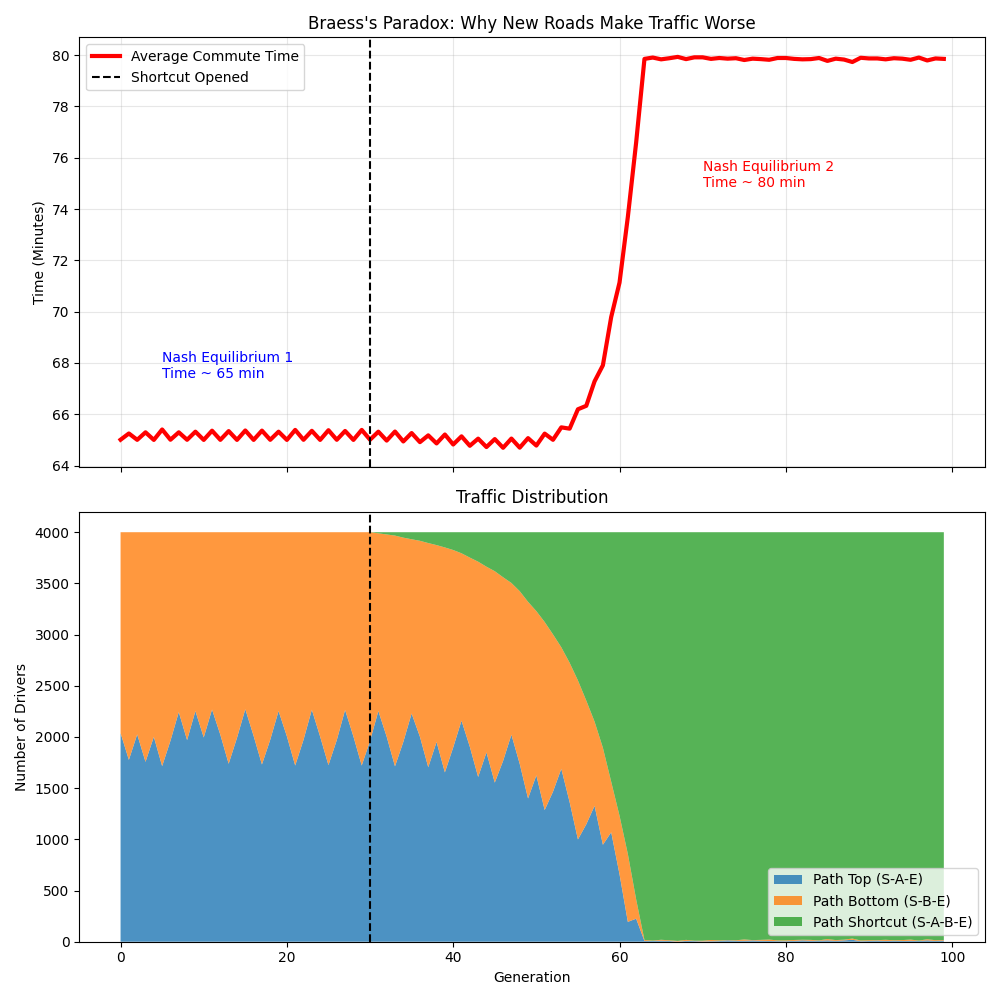
模拟结果

阶段一：平衡 (Generation 0 - 30)

流量分布：Top (蓝色) 和 Bottom (橙色) 各占一半，约 2000 人。
通勤时间：稳定在 65 分钟。
- 拥堵段耗时 $2000/100 = 20$。总耗时 $20 + 45 = 65$。
此时系统处于纳什均衡。没人想换路，因为换了也不会变快。

阶段二：捷径开放 (Generation 30)

最初反应：走捷径耗时更短。
- 捷径包含两段拥堵路。第一段 $2000/100=20$，第二段 $2000/100=20$。中间是 0。总和 $20+20=40$。小于 65 分钟。
- 部分个体从 Top 和 Bottom 转向 Shortcut。
- 随着绿色区域（Shortcut）急剧扩大，蓝橙区域消失。
最终结局 (Generation 50+)：
- 几乎所有 4000 人都挤在了 Shortcut 上。
- 流量分布：Top 和 Bottom 几乎为 0，Shortcut 接近 4000。
- 捷径包含两段拥堵路。第一段 $4000/100=40$，第二段 $4000/100=40$。中间是 0。总和 $40+40=80$。
回不去？
- 假设你想回到 Top 路。
- 时间 = 第一段拥堵 (40) + 第二段畅通 (45) = 85 分钟 > 80分钟。
- 纳什均衡陷阱：没有人能单方面改变策略来获益。

这被称为无政府的代价 (Price of Anarchy)。在交通网络中，每个人都试图缩短自己的通勤时间（个体理性），结果却导致所有人的通勤时间都增加了（集体非理性）。

解决布雷斯悖论的唯一方法是中心化调控（比如政府强行关闭那条捷径，或者对捷径收取高额过路费），依靠个体自由选择是无解的。

智猪博弈 (Boxed pigs game)

智猪博弈用于分析不对称收益结构下理性个体的策略选择，尤其展示了搭便车（free-riding）行为。

背景设定

一个狭长的箱子（或猪圈），一端有一个按钮，另一端有一个食物出料口。
箱子里有两只猪：一只大猪和一只小猪。
规则：
1. 按下按钮后，10 单位食物会从另一端掉出。
2. 但按按钮的猪需要跑过去按按钮，再跑回来吃食，这个过程会消耗2单位能量（相当于成本）。
3. 如果两只猪都去按按钮，大猪抢得多：大猪吃 7，小猪吃 3。
4. 如果只有小猪按按钮，大猪守在食槽：大猪吃 9，小猪跑回来只能吃到 1。
5. 如果只有大猪按按钮，小猪守在食槽：大猪跑回来吃到 6，小猪吃到 4。
6. 如果都不按，都得 0。

关键点：按按钮有成本，且收益分配不对称（大猪更强，能抢更多食物）。

	小猪：按按钮	小猪：等待
大猪：按按钮	大猪: 7−2=5 小猪: 3−2=1	大猪: 6−2=4 小猪: 4
大猪：等待	大猪: 9 小猪: 1−2=−1	大猪: 0 小猪: 0

纳什均衡

如果大猪选按按钮 → 小猪选等待。
如果大猪选等待， → 小猪选等待。

小猪的严格占优策略是“等待”（无论大猪怎么做，等都更好）。

如果小猪选择 按按钮 → 大猪会选择等待。
如果小猪选择等待 → 大猪会选择按按钮。

给定小猪等待，大猪的最优反应是按按钮。

唯一的纳什均衡：
（大猪按按钮，小猪等待）

弱者搭便车：小猪理性选择等待，让强者付出成本。
强者被迫行动：尽管大猪吃亏（净得 4，而小猪白得 4），但如果不行动，双方都得 0，所以只能承担成本。

企业中：大公司承担研发成本，小公司模仿获利。
国际政治：大国维护国际秩序，小国享受公共品。
公共品提供：富人捐款，穷人依赖。

布莱克韦尔定理 (Blackwell’s Theorem, 1951)

在什么情况下，我们可以毫无争议地说信息源 Q 比信息源 P 更好？

定理

对于任意两个实验 $P$（一个 $n \times m$ 矩阵）和 $Q$（一个 $n \times m’$ 矩阵），以下命题是等价的：

(a) 对于任意的 $U$ 和任意的 $p$，都有 $F(Q, U, p) \ge F(P, U, p)$。
无论决策问题 $U$ 和先验概率 $p$ 是什么，实验 $Q$ 带来的期望价值总是大于或等于实验 $P$。
(b) 对于任意的 $U$，都有 $B(Q, U) \supseteq B(P, U)$。
基于 $Q$ 的可行收益集合包含基于 $P$ 的可行收益集合。
(c) $C(Q) \supseteq C(P)$。
$Q$ 所生成的凸集包含 $P$ 所生成的凸集。
(d) 存在一个 $m’ \times m$ 的行随机矩阵 (row stochastic matrix) $M$，使得 $P = QM$。
$P$ 可以通过对 $Q$ 进行随机变换——即“混淆”或“加噪”——来得到。

$n$：世界的状态数（States of nature）。
$m$ 和 $m’$：实验观测到的信号/结果的数量（Signals）。
$P$ 和 $Q$：代表两个“实验”或“信息结构”的矩阵。
- 矩阵的行代表真实状态，列代表观测到的信号。
- 元素 $P_{ij}$ 表示“在状态 $i$ 下观测到信号 $j$ 的概率”。

四个等价条件

这个定理最强大的地方在于它建立了经济价值（条件 a）与统计结构（条件 d）之间的等价关系。

(a) 经济价值 (Value of Information)

$F(Q, U, p) \ge F(P, U, p)$ for any $U$ and any $p$.

含义： 对于任何先验概率 $p$ 和任何效用函数（决策问题）$U$，基于实验 $Q$ 做出的决策，其期望收益永远大于或等于基于实验 $P$ 做出的决策。
直觉： $Q$ 是一个更有价值的信息源。无论你想做什么（$U$）以及你原本怎么看世界（$p$），$Q$ 都能让你做得比 $P$ 更好（或至少一样好）。

(b) & (c) 几何/集合性质 (Feasible Sets)

(b) $B(Q, U) \supseteq B(P, U)$ (c) $C(Q) \supseteq C(P)$

含义： 这两个条件从几何角度描述了信息。$C(P)$ 通常指的是由 $P$ 的行向量生成的凸包（Convex Hull）或相关的后验概率分布集合。
直觉： $Q$ 能产生的后验概率分布的范围比 $P$ 更广。
- 想象一下，$P$ 提供的信息很模糊，你的后验概率总是接近先验概率（聚集在中间）。
- 而 $Q$ 提供的信息很精准，能让你的后验概率剧烈变化（更接近 0 或 1）。因此，$Q$ 的“分布范围”包含了 $P$ 的范围。

(d) 统计结构：混淆 (Garbling)

There exists a row stochastic matrix $M$ such that $P = QM$.

含义： 这是定理中最核心的结构性定义。它说 $P$ 仅仅是 $Q$ 的一个“混淆” (Garbling)。
物理过程解释：
1. 先进行实验 $Q$，得到一个信号。
2. 然后根据矩阵 $M$（代表噪声或随机化处理），把这个信号转换一下。
3. 得到的结果在统计上就等同于实验 $P$。
直觉： $P$ 就是“加了噪声”的 $Q$。既然 $P$ 是 $Q$ 的降级版，那么 $Q$ 包含的信息量一定涵盖了 $P$。

证明思路 (Sketch of Proof)

证明的核心在于证明 (d) $\Rightarrow$ (a) 和 (a) $\Rightarrow$ (d)。

第一部分：(d) $\Rightarrow$ (a) （比较简单，直觉驱动）

命题： 如果 $P$ 是 $Q$ 的混淆（即 $P = QM$），那么 $Q$ 对任何决策者都更有价值。

证明逻辑：

假设你只能观察到实验 $Q$ 的结果。
如果你想用实验 $P$ 来做决策，你完全可以自己“模拟”出 $P$。
方法是：当你看到 $Q$ 的输出信号 $y$ 时，你自己掷一个骰子（根据概率矩阵 $M$），生成一个模拟信号 $z$。根据矩阵乘法定义，这个 $z$ 的统计分布和真实的实验 $P$ 完全一样。
这意味着：凡是基于 $P$ 能达到的期望收益，基于 $Q$ 也一定能达到（只要我在 $Q$ 后面人为加上噪声 $M$ 就能复现 $P$ 的策略）。
此外，基于 $Q$ 我还可以选择“不加噪声”，直接利用更纯净的信息，这可能会带来更高的收益。
结论：$F(Q) \ge F(P)$。

第二部分：(a) $\Rightarrow$ (d) （比较困难，需要凸分析）

命题： 如果对于所有决策问题，$Q$ 的价值都比 $P$ 高，那么 $P$ 一定等于 $Q$ 乘以某个随机矩阵。

证明逻辑（利用分离超平面定理）：

我们将实验看作是状态空间到概率分布空间的映射。
利用条件 (c) 作为中间桥梁。凸分析告诉我们，任何凸函数（比如期望效用函数通常是关于后验概率的凸函数）的性质与定义域的几何形状有关。
如果 $F(Q) \ge F(P)$ 对所有凸函数（效用函数）成立，根据Hardy-Littlewood-Pólya 不等式或谢尔曼-斯坦因定理 (Sherman-Stein Theorem) 的推广，这意味着 $P$ 的行向量必须落在 $Q$ 的行向量的凸包内部（或者存在某种受控Majorization关系）。
数学上，这等价于说 $P$ 的每一行都可以表示为 $Q$ 的行的线性组合，且系数非负和为1（这就是随机矩阵 $M$ 的定义）。
因此，存在一个随机矩阵 $M$ 使得 $P = QM$。

其他

如果有人试图卖给你一份情报（实验 $P$），你应该问：这份情报是否只是我在现有情报（实验 $Q$）上加点噪声就能得到的？如果是，那么 $P$ 就不如 $Q$。
如果两种实验 $P$ 和 $Q$ 之间不存在 $P=QM$ 或 $Q=PM$ 的关系，那么它们就是不可比的。也就是说，对于某些任务 $P$ 更好，而对于另一些任务 $Q$ 更好。

贝叶斯劝说 (Bayesian Persuasion)

Kamenica & Gentzkow (2011) 开创的领域。

作为发信人（Sender），我该如何设计信息披露规则，来操纵收信人（Receiver）的信念，从而让他做出对我最有利的行为？
不撒谎，但可以通过模糊信息的精度来获利。

经典例子：检察官与法官 (The Judge and The Prosecutor)

设定：

参与者：检察官（Sender）想让嫌疑人被定罪；法官（Receiver）想公正判决。
状态：嫌疑人要么是有罪（Guilty, G），要么是无辜（Innocent, I）。
先验概率：嫌疑人有罪的概率是 30% ($P(G)=0.3$)，无辜是 70%。
法官的规则：只有当“嫌疑人有罪的概率”超过 50% 时，法官才会判决定罪；否则释放。
检察官的收益：只要定罪得 1 分，释放得 0 分（不管是否真的有罪）。

场景 1：不做任何调查（无信息）

法官只看先验概率：30% 有罪。
30% < 50%，法官判释放。
检察官收益：0。

场景 2：完全信息（彻查出真相）

调查结果完全揭示真相。
30% 的案子显示确凿有罪 $\rightarrow$ 法官定罪。
70% 的案子显示确凿无辜 $\rightarrow$ 法官释放。
检察官收益：0.3。

场景 3：最优信息设计（Bayesian Persuasion）

检察官设计一种含糊其辞的调查报告机制（信号结构），比如只调查某些特定证据。他承诺总是如实展示调查结果。

他设计两个信号：看起来有罪 (High) 和 看起来无辜 (Low)。构造如下概率分布：

如果嫌疑人真的有罪：100% 发出信号 High。
如果嫌疑人真的无辜：$\frac{3}{7}$ 的概率发出信号 High，$\frac{4}{7}$ 的概率发出信号 Low。

法官视角（贝叶斯更新）：

当法官看到信号 Low：
- 后验概率： $P(G|Low) = \frac{P(Low|G)P(G)}{P(Low|G)P(G) + P(Low|I)P(I)}$ $= \frac{0 \times 0.3}{0 \times 0.3 + \frac{4}{7} \times 0.7}$ $= 0$
- 这意味着嫌疑人绝对是无辜的（因为有罪者不会发出 Low）。
- 判决：释放。
当法官看到信号 High：
- 后验概率： $P(G|High) = \frac{P(High|G)P(G)}{P(High|G)P(G) + P(High|I)P(I)}$ $= \frac{1 \times 0.3}{1 \times 0.3 + \frac{3}{7} \times 0.7}$ $= \frac{0.3}{0.3 + 0.3} = 0.5$
- （注：检察官会让这一概率 $\epsilon$ 优于阈值）。
- 此刻，嫌疑人有罪的概率恰好达到或略超过 50%。
- 法官按照规则判决：定罪。

结果分析：

发出信号 “High” 的总频率是多少？ $0.3 (来自有罪) + 0.7 \times \frac{3}{7} (来自无辜) = 0.3 + 0.3 = 0.6$。
检察官的期望收益：0.6。

结论：

无信息收益 = 0
完全信息收益 = 0.3
信息设计收益 = 0.6

检察官通过“把所有真正的罪犯”和“一部分倒霉的无辜者”混在一起（Pooling），刚好凑到了法官的心理底线（50%），从而最大化了定罪率。这就是利用 Blackwell 意义上“较差”的信息（不完全揭示真相），实现了自身利益最大化。

魔法/戏法？

如果嫌疑人明明是无辜的，检察官却设计了一个机制让他有 $3/7$ 的概率被标记为看起来有罪，这难道不是栽赃陷害（撒谎）吗？

贝叶斯劝说（Bayesian Persuasion）模型的一个核心假设是：接收者（法官）是知道检察官所使用的调查规则的。

撒谎（Lying / Cheap Talk）：检察官做完调查，发现嫌疑人无辜，然后伪造一份证据，告诉法官“他有罪”。
- 结果：如果法官知道检察官可能会撒谎，法官就不会相信检察官说的任何话（信号失去效力）。
信息设计（Information Design）：检察官在调查开始之前，选择了一种“特定的调查仪器”或“调查范围”。
- 检察官：“我决定使用一个灵敏度(召回率 TPR)极高、但误报率(FPR)也很高的测谎仪。”
- 关键点：一旦选定了这个仪器，检察官必须诚实地向法官展示仪器的读数。如果仪器（哪怕是因为误报）响了，检察官就如实提交“仪器响了”的报告。

那个 $3/7$ 的概率，代表的是误报率(False Positive Rate)。检察官并没有捏造证据，他只是故意选择了一个很容易产生误报的调查方法。

在这个模型中，法官是完全理性且知情的。法官知道检察官用的这个调查方法有 $3/7$ 的概率冤枉好人。

那法官为什么还买账？因为法官不仅看误报率，还看贝叶斯更新后的总概率。

请看这个逻辑链：

法官想：“我知道这个调查方法很烂，好人也有 $3/7$ 的概率被它标记为 High。”
法官继续想：“但是，如果嫌疑人是真的罪犯，他是 $100\%$ 被标记为 High 的。”
法官的结论：“所以，尽管这个信号有水分，但看到 High 信号时，嫌疑人有罪的概率（50%）依然比什么都没看到时的概率（30%）要高。既然达到了我 50% 的判决门槛，按照规则，我必须判决有罪。”

这正是检察官的狡猾之处： 他没有撒谎说“这人 100% 有罪”，他只是提供了一个“含混”的信号，把概率从 30% 推到了 50%。他利用了法官的规则（只要 >50% 就判），而不是欺骗法官的认知。

为了证明检察官没有“凭空捏造”，Blackwell 定理和信息设计理论有一个铁律，叫做 贝叶斯可信性。

无论你如何设计信号，所有信号导致的后验概率的期望值，必须等于先验概率。

验算一下检察官有没有“作弊”：

先验概率（没调查前）：有罪率 = 0.3。
后验概率（调查后）：
- 发出 High 信号（判有罪）：此时法官认为有罪率为 0.5
  - \[P(G|High) = 0.5\]
  - \[P(High) = P(High|G)P(G) + P(High|I)P(I) = 0.3 \times 1 + 0.7 \times \frac{3}{7} = 0.6\]
- 发出 Low 信号（判释放）：此时法官认为有罪率为 0
  - \[P(G|Low) = 0\]
  - \[P(Low) = P(Low|G)P(G) + P(Low|I)P(I) = 0.7 \times \frac{4}{7} = 0.4\]
求期望值： $P(G) = 0.5 \times 0.6 + 0 \times 0.4 = 0.3$

这意味着，检察官并没有从整体上改变世界的真相。他所做的，只是把概率进行了重新分配。他把那些“看起来有点像有罪的无辜者”（那 3/7），和“真正的罪犯”混合在了一起，打包卖给了法官。

但在博弈论中：

撒谎 = 只有红球，我硬说是黑球。
信息设计 = 我拿一个很脏的玻璃罩住球，让你透过脏玻璃看。红球看起来肯定是红的，但白球透过脏玻璃看起来也像红的（粉红）。

检察官没有改色，他只是选了一块最脏的玻璃，脏到刚好能让你信服，又不至于让你完全看不清。这就是操纵信念的艺术。

新判决规则

检察官之所以能得逞，根本原因在于法官的判决规则对于检察官来说是已知的、固定的，且是不完美的。

在法理学和统计学中，阈值取决于我们对犯错的容忍度。

第一类错误 (Type I Error)：冤枉好人（把无辜判为有罪）。
第二类错误 (Type II Error)：放纵坏人（把有罪判为无辜）。

贝叶斯决策： $阈值 P^* = \frac{Cost_{I}}{Cost_{I} + Cost_{II}}$

判决规则50%中隐含的假设是：法官认为冤枉好人和放纵坏人的代价是一样的。

现实中，刑法讲究排除合理怀疑（Beyond Reasonable Doubt）: 冤枉好人的代价远大于放纵坏人。

假设法官把标准提高到 90%（即：只有嫌疑人有罪概率 > 90% 才判）。

检察官还能“操纵”吗？能，但赚得少了。

检察官需要重新设计信号，减少混入的无辜者比例（把玻璃擦得干净一点），使得当信号 High 出现时，有罪概率刚好达到 90%。

计算： $P(G|High) = \frac{0.3}{0.3 + P(High|I) \times 0.7} = 0.9$ 解得：$P(High|I) \approx 0.047$
结果：检察官只能把 4.7% 的无辜者拉下水（之前是 43%）。总定罪率 = $0.3 + 0.7 \times 0.047 \approx 33\%$。
迫使检察官使用误报率低(FPR)的调查方式

机制设计

机制设计常被称为反向博弈论 (Reverse Game Theory)。

传统博弈论：给定游戏规则（博弈结构），预测玩家会做什么（均衡结果）。
机制设计：给定想要达到的结果（社会目标），设计一套游戏规则（机制），使得玩家在自利驱动下博弈出的结果，恰好符合设计者的目标。

激励相容 (Incentive Compatibility, IC)

激励相容是机制设计中最基本的约束条件。

在一个机制中，如果对于每一个参与者而言，按照设计者希望的方式行动（通常指如实报告私人信息）是其最优策略，那么该机制就是激励相容的。

参与者拥有设计者所不知道的私人信息（Type, $\theta$）。设计者希望根据这些信息做出社会最优决策。但如果说真话会损害参与者的利益，他们就会撒谎。

约束公式：$U(\text{说真话}) \geq U(\text{撒谎})$
分类：
- 占优策略激励相容 (DSIC)：无论别人怎么做，我最好的策略都是说真话（最强要求，如第二价格拍卖）。
- 贝叶斯激励相容 (BIC)：给定我对别人类型的概率预判，我说真话的期望收益最大。

设计者不能强迫参与者做好事，必须设计规则让做好事（比如不隐瞒成本、不虚报估值）成为参与者为了自身利益最大化而不得不做出的选择。

个体理性 (Individual Rationality, IR) / 参与约束 (Participation Constraint)

参与者参与这个机制得到的期望效用，不能低于他不参与时的保留效用（Reservation Utility）。

除了要防撒谎（IC），还要防掀桌子走人。一个好的机制必须让大家觉得值得一玩。

显示原理 (Revelation Principle)

任何一个能够通过某种复杂机制（间接机制）实现的均衡结果，都可以通过一个直接显示机制 (Direct Revelation Mechanism) 且具备激励相容 (IC) 性质来实现。

大幅简化问题

在寻找最佳机制时，设计者面临的困难是“机制”的形式是无穷无尽的（可以是拍卖、投票、复杂的谈判流程等）。

显示原理的作用：它告诉我们，不需要去搜索所有可能的复杂游戏规则。
结论：我们只需要关注一类特殊的机制——直接机制（Direct Mechanism），即只询问参与者“你的类型是什么？”，并且只需关注那些让参与者愿意说真话（IC）的机制。
数学意义：它将一个在无限函数空间中寻找最优解的问题，转化为在满足 IC 约束（通常是一组不等式）的集合中寻找最优解的数学规划问题。

我们定义以下符号：

$\theta$：参与者的类型（私人信息）。
$M = (S, g)$：一个间接机制（复杂的规则）。
- $S$：策略空间（比如报价、投票、谈判动作）。
- $g(s)$：结果函数（给定动作 $s$，最后发生什么）。
$s^(\theta)$：参与者在间接机制下的最优均衡策略。即：当我是类型 $\theta$ 时，我选择动作 $s^(\theta)$ 能让我收益最大。

显示原理的构造过程：

设计者构建一个新的直接机制 $M_{dir} = (\Theta, f)$：

询问：直接问参与者的类型 $\hat{\theta}$（参与者报告的类型，可能撒谎）。
映射规则：$f(\hat{\theta}) = g(s^*(\hat{\theta}))$。
- 新机制的规则是——“你告诉我你是 $\hat{\theta}$，我就去查表看看你在老游戏里会做什么动作 $s^*(\hat{\theta})$，然后我直接给你那个老游戏的结果”。

证明它是激励相容 (IC) 的： 在原游戏 $M$ 中，因为 $s^*(\theta)$ 是均衡策略，这意味着：

\[U(g(s^*(\theta)), \theta) \ge U(g(s'(\theta)), \theta) \quad \text{对于任何其他策略 } s'\]

特别地，如果不按 $\theta$ 出牌，而是模仿类型 $\hat{\theta}$ 的打法 $s^*(\hat{\theta})$，肯定没有原策略好：

\[U(g(s^*(\theta)), \theta) \ge U(g(s^*(\hat{\theta})), \theta)\]

把上面这个不等式代入新机制 $f$ 的定义（因为 $f(\cdot) = g(s^*(\cdot))$）：

\[U(f(\theta), \theta) \ge U(f(\hat{\theta}), \theta)\]

含义：报告真实类型 $\theta$ 的收益 $\ge$ 报告虚假类型 $\hat{\theta}$ 的收益。

实施理论 (Implementation Theory)

实施理论研究的是机制设计的一个更深层的问题：“唯一性”与“多重均衡”。

仅仅设计一个机制，使得“设计者想要的目标”是该机制的一个均衡结果（这叫弱实施）是不够的，因为该机制可能还存在其他坏的均衡。

核心问题：给定一个社会选择函数（目标），是否存在一个机制，使得该机制的所有可能的均衡结果都对应于该社会选择函数？
完全实施 (Full Implementation)：设计出的机制不仅要让好结果成为均衡，还要排除掉所有不想要坏均衡。

案例：单物品拍卖

场景设置：

设计者：拍卖行（目标是社会效率最大化，即将物品卖给评价最高的人）。
参与者：Alice ($v_A=100$) 和 Bob ($v_B=80$)。这些估值是他们的私人信息（Type, $\theta$）。
挑战：拍卖行不知道谁的估值高，需要设计规则。

幼稚机制

幼稚机制：拍卖行直接问：“你们愿意出多少钱？出得高的得，并支付报价。”（即第一价格拍卖）。
博弈论分析：
- Alice 绝不会报 100。如果她报 100，即便赢了，收益为 $100 - 100 = 0$。
- 她会进行策略性撒谎（Bid Shading）。比如她猜 Bob 会出 80 左右，她可能出 81。
- 结果：设计者发现很难预测结果，因为结果取决于 Alice 对 Bob 的猜想。如果 Alice 猜错（比如以为 Bob 只出 50，于是她出 51），结果可能导致效率损失或收益不稳定。
机制设计目标：我们需要设计一种规则，使得“把物品给评价最高的人”成为必然结果。

显示原理的应用

设计者面临无数种拍卖规则的选择（第一价格、全支付拍卖、蜡烛拍卖等）。

显示原理：只需要寻找某种直接机制，让大家愿意说真话即可。

原机制（间接）：第一价格拍卖。Alice 的最优策略是 $s^*(\theta) = \theta - \epsilon$（把价格报低一点）。
构造直接机制：设计者对 Alice 说：“你别自己费脑筋算该把价格报低多少了。你直接把心里的真话 $100$ 告诉我。由于我知道在第一价格拍卖里你会报 $81$，我替你把 $81$ 这个数字填进标书里。”
结论：显示原理保证了，只要存在一种复杂的拍卖能卖对人，就一定存在一种“直接让大家报真价”的机制也能卖对人。我们将目光锁定在寻找激励相容的直接机制上。

激励相容 (IC) 与个体理性 (IR) 的实现：维克里拍卖

为了满足直接机制中的 IC 和 IR，设计者选用了第二价格拍卖 (Vickrey Auction)：出价最高者得，但只需支付第二高的价格。

检验激励相容 (IC)： Alice 真实值 $v_A=100$。

说真话（报 100）：Bob 报 80。Alice 赢，付 80。净收益 = 20。
撒谎报高（报 200）：Bob 报 80。Alice 赢，付 80。净收益 = 20（没变好）。
撒谎报低（报 90）：Bob 报 80。Alice 赢，付 80。净收益 = 20（没变好）。
撒谎报太低（报 70）：Bob 报 80。Alice 输。净收益 = 0（变差了）。
结论：无论 Bob 怎么做，Alice 说真话 $100$ 都是占优策略 (DSIC)。IC 约束满足。

检验个体理性 (IR)：

如果 Alice 赢了，说明她的估值 > 第二高价格。收益 $U = v_A - P_{2nd} > 0$。
如果 Alice 输了，收益为 0。
结论：参与总是比不参与好（至少不亏），IR 约束满足。

实施理论的挑战

虽然第二价格拍卖满足了 IC，看起来很完美，但实施理论提醒我们注意多重均衡的问题。

设计者希望的均衡是：Alice 报 100，Bob 报 80。Alice 赢。这是好均衡。

但是，这个机制下可能存在一个坏均衡（纳什均衡，非占优策略均衡）：

Alice 策略：报 0。
Bob 策略：报 1000。
结果：Bob 赢，支付 0。Alice 输。
分析：
- 对于 Bob：既然 Alice 报 0，我报 1000 能赢且只需付 0，非常爽。
- 对于 Alice：既然 Bob 报了 1000，我若想赢必须报 >1000。但我估值才 100，赢了要付 1000，亏死。所以我干脆报 0，输了拉倒。
- 双方都没有动力单方面改变策略。这就是一个均衡。

实施理论的意义：仅仅设计出维克里拍卖（第二价格）实现了弱实施（好结果是均衡之一），但没有实现完全实施（因为存在上述坏均衡，导致物品给了估值低的 Bob）。

为了解决这个问题，设计者可能需要引入保留价格 (Reserve Price) 或者修改规则来剔除这个坏均衡，确保唯一的结果就是社会最优的结果。

VCG 机制 (Vickrey-Clarke-Groves Mechanism)

分类：公共品供给 / 外部性内化

Vickrey拍卖只是VCG机制的一个特例。VCG是解决多人协作与公共决策最通用的理论框架。

克拉克税 (Clarke Tax) ：你只需要支付因为你的存在而给其他人造成的麻烦。

如果没有你，结果和现在一样 $\rightarrow$ 你没有造成麻烦 $\rightarrow$ 你不付钱。
如果没有你，结果变了（比如本来不修桥，因为你来了所以修了） $\rightarrow$ 你是关键人物 (Pivotal) $\rightarrow$ 你要补齐其他人（包括出资方）的净损失。

假设小区里有三个邻居：A, B, C。政府提议修一个路灯，总成本是 100 元。政府问三人：“这路灯对你们值多少钱？”（大家心里有数，但可能会撒谎）。

每个人的真实内心估值如下：

A (怕黑)：70 元
B (喜欢亮)：60 元
C (无所谓)：10 元

社会总账：

总估值：$70 + 60 + 10 = 140$ 元。
总成本：$100$ 元。
决策：$140 > 100$，应该修路灯（社会最优结果）。

Clarke Tax：[你的税] = [没有你时其他人的总福利] - [有你时其他人的总福利]

1. 计算 A 的税费

假设 A 不在：
- 剩下 B + C 的估值 = $60 + 10 = 70$ 元。
- $70 < 100$ (成本)。
- 结果：路灯不修。
- 其他人的福利：$0$ (没修灯，没收益，也没成本)。
现在 A 在场：
- 结果：路灯修了。
- 其他人的福利：(B得到了60) + (C得到了10) - (社会付出的成本100) = -30。
A 造成的麻烦 (外部性)：
- A 的出现，强行推动了一个让其他人亏损 30 元的项目（虽然加上 A 是赚的，但光看 B+C和成本方是亏的）。
- A 的税 = $0 - (-30) = \mathbf{30}$ 元。

验证：A 收益 70，付税 30，净赚 40。A 很高兴。

2. 计算 B 的税费

假设 B 不在：
- 剩下 A + C 的估值 = $70 + 10 = 80$ 元。
- $80 < 100$。
- 结果：路灯不修。
- 其他人的福利：$0$。
现在 B 在场：
- 结果：路灯修了。
- 其他人的福利：(A得到了70) + (C得到了10) - (社会成本100) = -20。
B 的税：
- B 的存在也改变了结果，他也让其他人净亏了 20 元。
- B 的税 = $0 - (-20) = \mathbf{20}$ 元。

验证：B 收益 60，付税 20，净赚 40。B 也很高兴。

3. 计算 C 的税费

假设 C 不在：
- 剩下 A + B 的估值 = $70 + 60 = 130$ 元。
- $130 > 100$。
- 结果：路灯照样修！
- 其他人的福利：(A+B的收益 130) - (成本 100) = 30。
现在 C 在场：
- 结果：路灯修了。
- 其他人的福利：(A+B的收益 130) - (成本 100) = 30。
C 的税：
- $30 - 30 = \mathbf{0}$ 元。

结论：C 不是“关键人物 (Pivotal)”。无论 C 是否参与，路灯都会修。C 没有给其他人造成额外的负担或改变结果，所以 C 一分钱都不用出，但可以享用路灯。

为什么这个机制能防撒谎 (IC)？

在 Clarke Tax 下，你的支付金额只和别人的报价有关，和你自己的报价无关（只要你的报价不改变最终修/不修的结果）。

试探 1：A 想少付钱，故意报低？

A 本来要付 30。他想：“要是报低点，是不是付得少？”
假如 A 撒谎报 40（原本是 70）。
总报价 = $40(A) + 60(B) + 10(C) = 110 > 100$。还是修。
A 的税费计算：取决于 (B+C) 和成本。这两项都没变。所以 A 还是付 30。
结果：撒谎没能降低税费。

试探 2：A 报得太低，导致不修了？

假如 A 撒谎报 20。
总报价 = $20 + 60 + 10 = 90 < 100$。不修了。
A 的结局：路灯没修，收益为 0，税费为 0。
对比：说真话时，A 净赚 40。
结果：撒谎导致 A 亏了（失去了原本能赚到的效用）。

试探 3：C 想捣乱，故意报高？

C 是不关键人物，付 0。
假如 C 撒谎报 100（原本是 10）。
总报价变高了，当然还是修。
C 的税费计算：
- 没 C 时：A+B=130，修。社会净福利 30。
- 有 C 时：A+B+Cost = 30。
- C 还是付 0。
结果：撒谎没好处，也没坏处（但在严格定义下，说真话是弱占优策略）。

其他

A 和 B 是关键人物 (Pivotal)：没了他们项目就黄了，所以他们必须补偿因为项目上马而产生的社会成本缺口。
C 是非关键人物：他在不在项目都会上马，所以他免费享受。
支付总额：$30 + 20 + 0 = 50$ 元。
- 注意：修路灯成本是 100，收上来的税只有 50。这说明 Clarke Tax 不是用来筹集工程款的。
- 这 50 元甚至不能分给参与者，必须捐给毫不相关的慈善机构。如果分给参与者，就会破坏激励机制。
- 差额的工程款通常需要通过之前的定额税或其他方式补齐。机制设计的重点是让大家说实话以做正确的决定，而不是如何分摊成本。

盖尔-沙普利算法 (Gale-Shapley Algorithm) / 延迟接受算法 (DA)

分类：双边匹配 (Two-Sided Matching) / 无金钱机制

这是机制设计在没有货币转移情况下的应用（获诺贝尔奖），解决了如“医生-医院匹配”、“高考志愿录取”等问题。

场景：医学院毕业生找实习医院，医院招毕业生。双方都有自己的偏好排名（私人信息）。
难题：如果允许私下接触，会出现不稳定 (Unstable) 的匹配。即：医生A去了医院B，但其实A更想去医院C，而C也觉得A比它现在的招的人好。这样A和C就会私奔，破坏系统。
机制规则 (以医生申请为例)：
1. 第一轮：每个医生向自己最喜欢的医院申请。医院在收到的申请中，暂时保留最好的，拒绝其他的。
2. 第二轮：被拒绝的医生向自己第二喜欢的医院申请。医院将新收到的申请与手中暂时保留的进行比较，保留最好的，拒绝其他的。
3. 如此往复，直到没有医生再被拒绝。
为何成功：
- 稳定性：该机制保证结果是稳定的（不存在愿意私奔的对子）。
- IC性质：对于主动提出申请的一方（医生），说真话（按真实喜好排名）是占优策略 (DSIC)。
- 注：对于被动接受的一方（医院），说真话不一定是占优策略，这体现了机制设计的局限性。

航司定价与非线性定价 (Second-Degree Price Discrimination)

分类：筛选机制 (Screening) / 隐藏信息

这是显示原理在商业中最直观的应用。设计者（航司）不知道谁是商务客（有钱、时间紧），谁是旅游客（没钱、时间宽裕）。

场景：卖机票。
- 类型 $\theta_{high}$：愿意出高价，不能忍受转机/退改签限制。
- 类型 $\theta_{low}$：只愿出低价，能忍受限制。
机制设计：
- 不能直接问“你是富人吗？”，富人会撒谎说自己是穷人来买便宜票。
- 设计两个“合同包”：
  - $C_1$：{高价，直飞，随时退改}
  - $C_2$：{低价，转机，不可退改，座位窄}
IC 约束的应用：
- 为了让富人自愿买 $C_1$，必须故意恶心一下 $C_2$（比如增加转机时间、扣除里程积分）。
- 必须满足：$U_{\text{富}}(C_1) \geq U_{\text{富}}(C_2)$。
- 结论：为了实现分离均衡（让富人说真话），机制设计者必须人为制造低效（让经济舱变得不够舒服），以防止富人伪装成穷人。这被称为为了信息租金而牺牲效率。

所罗门的审判 (King Solomon’s Dilemma)

场景：两个女人争一个孩子，都说是自己的。
- 真母亲：想要孩子，对孩子的估值很高，记为 $V_{高}$（比如 100万元）。
- 假母亲：想要孩子，对孩子也有估值（也许是想卖掉，也许是有一点感情），但肯定比亲妈低，记为 $V_{低}$（比如 20万元）。
- 理性的参与者：两人都是极其聪明的，都会为了自己的利益最大化而行动。
朴素机制：所罗门问：“谁是妈？” -> 两人都举手。机制失效。
所罗门的新机制：
- 设定一个价格 $P$（比如 30万元）。这个价格很精妙，介于两人估值之间：$V_{低} < P < V_{高}$。
- 设定一个巨额罚款 $F$（比如 1000万元），这是用来惩罚撒谎者的。

在博弈论和机制设计中，机制的规则必须是完全公开 (Public) 且共同知识 (Common Knowledge) 的。

与圣经故事里的“突然袭击”完全不同(假设人是情绪化的，且不知道判决标准)。

“听好了，规则如下：A 先说。如果 A 说是，B 可以反对。如果 B 反对，B 花 30 万买走孩子，同时 A 罚款 1000 万。你们听懂了吗？好，游戏开始。”

假设人是绝对理性的，且完全掌握游戏规则。

情况一：假设 A 是真母亲，B 是假母亲

先看第二阶段（B 的选择）：
- 假如 A 说了“是我的”，轮到 B 选。
- 如果 B 选择“反对”：B 必须花 30万($P$) 买走估值只有 20万($V_{低}$) 的孩子。
- B 的收益 = $20万 - 30万 = -10万$。
- 如果 B 选择“同意”：收益为 0。
- 结论：理性的假母亲 B 不反对。
再看第一阶段（A 的选择）：
- 真母亲 A 能够预判到B 不反对。
- 所以 A 放心大胆地说“是我的”。
- 结果：A 得到孩子，没花钱。符合目标。

情况二：假设 A 是假母亲，B 是真母亲

先看第二阶段（B 的选择）：
- 假如 A 撒谎说了“是我的”，轮到 B 选。
- 如果 B 选择“反对”：B 花 30万($P$) 买走估值 100万($V_{高}$) 的孩子。
- B 的收益 = $100万 - 30万 = +70万$。
- 如果 B 选择“同意”：眼睁睁看着孩子给别人，收益 0。
- 结论：理性的真母亲 B 一定会反对。
再看第一阶段（A 的选择）：
- 假母亲 A 预判到：如果我说“是我的”，B 一定会反对。
- 一旦 B 反对，A 就要交巨额罚款 $F$ (-1000万)。
- 相比之下，如果 A 一开始就承认“不是”，虽然得不到孩子，但至少不用罚款（收益 0）。
- 结论：假母亲 A 会在第一阶段这就自动放弃，说“不是”。
- 结果：B 得到孩子。符合目标。

蛋糕切分（或和尚分粥）

如果蛋糕由母亲来分配，无论母亲怎么分蛋糕，都很可能导致其中一个孩子满意，而另一个生气。（蛋糕可能某部分有樱桃，某部分奶油更多）

解决思路：蛋糕由其中一个小孩分，而另一个小孩则有优先选择拿哪一块的权利。（要让一个人诚实分割，必须让他承担分配不均的全部后果）

个体理性：参与这个游戏的结果，至少不会比“什么都拿不到”更差。

激励相容：对于切蛋糕的，最优策略（Dominant Strategy）是：尽可能地把蛋糕切成他眼里绝对公平的 50/50。激励相容：对于先选蛋糕的，最优策略（Dominant Strategy）是：优先选择他眼里绝对更好的那一份。

诚实（显示出私有信息）对两者来说都是最优策略。

合租分房间 & 分租金

设两人合租，两房间（大房、小房），总租金 $R = 3000$。
每位租户 $i \in {A, B}$ 对每个房间有私有估值 $V_{i, \text{room}}$，满足 准线性效用（Quasi-linear Utility）假设：

效用 = 主观价值 − 支付租金。

示例估值（单位：元）：

	大房	小房	总和
A	2000	1000	3000
B	1800	1200	3000

步骤 1：确定帕累托最优分配

计算两种分配方案的社会总福利（即估值之和）：

方案 1（A 大，B 小）：$2000 + 1200 = 3200$
方案 2（B 大，A 小）：$1800 + 1000 = 2800$

选择方案 1（A 住大房，B 住小房）为帕累托最优分配。

步骤 2：求解无怨价格区间（Envy-Free Zone）

设大房租金为 $x$，则小房租金为 $3000 - x$。
要求双方均无意愿交换房间。

A 的无怨条件（住大房）： $2000 - x \ge 1000 - (3000 - x) \Rightarrow x \le 2000$
B 的无怨条件（住小房）： $1200 - (3000 - x) \ge 1800 - x \Rightarrow x \ge 1800$

无怨区间：$x \in [1800, 2000]$

步骤 3：具体定价 —— 平分超额福利

选择区间中点以体现公平性：

$x = 1900$（大房租金）
小房租金 = $3000 - 1900 = 1100$

最终分配：

A：住大房，付 1900，效用 = $2000 - 1900 = 100$
B：住小房，付 1100，效用 = $1200 - 1100 = 100$

双方效用相等，均“占了便宜”，无怨且感知公平。

激励相容性不严格满足。

反例（策略性操纵）：
假设 B 真实估值为（1800, 1200），但因为知道A的估值，所以谎报为（1990, 1010）。

分配仍为 A 大、B 小（总福利更高）。
新无怨区间：$x \in [1990, 2000]$
中点定价：$x = 1995$ → B 付 $1005$（比诚实下的 1100 更少）

但若B对A的估值不准确，可能使得决策结果变化，最终所有人的福利都降低。

博弈论

博弈论演化

本文由作者按照 CC BY 4.0 进行授权

信任的演化（The Evolution of Trust）

最后通牒博弈（Ultimatum Game）

棋盘

生态系统

机会均等

自由选择

代际演化（自然选择, 适者生存）

求解

代码

运行结果

其他初始分布

蜈蚣博弈 (Centipede Game)

棋盘

规则设定

策略 (基因)

代码

运行结果

低生存压力

中生存压力

高生存压力

高生存压力+bonus

结论

布雷斯悖论 (Braess’s Paradox)

代码

模拟结果

阶段一：平衡 (Generation 0 - 30)

阶段二：捷径开放 (Generation 30)

智猪博弈 (Boxed pigs game)

背景设定

纳什均衡

布莱克韦尔定理 (Blackwell’s Theorem, 1951)

定理

四个等价条件

(a) 经济价值 (Value of Information)

(b) & (c) 几何/集合性质 (Feasible Sets)

(d) 统计结构：混淆 (Garbling)

证明思路 (Sketch of Proof)

第一部分：(d) $\Rightarrow$ (a) （比较简单，直觉驱动）

第二部分：(a) $\Rightarrow$ (d) （比较困难，需要凸分析）

其他

贝叶斯劝说 (Bayesian Persuasion)

经典例子：检察官与法官 (The Judge and The Prosecutor)

魔法/戏法？

新判决规则

机制设计

激励相容 (Incentive Compatibility, IC)

个体理性 (Individual Rationality, IR) / 参与约束 (Participation Constraint)

显示原理 (Revelation Principle)

实施理论 (Implementation Theory)

案例：单物品拍卖

幼稚机制

显示原理的应用

激励相容 (IC) 与 个体理性 (IR) 的实现：维克里拍卖

实施理论的挑战

VCG 机制 (Vickrey-Clarke-Groves Mechanism)

1. 计算 A 的税费

2. 计算 B 的税费

3. 计算 C 的税费

为什么这个机制能防撒谎 (IC)？

其他

盖尔-沙普利算法 (Gale-Shapley Algorithm) / 延迟接受算法 (DA)

航司定价与非线性定价 (Second-Degree Price Discrimination)

所罗门的审判 (King Solomon’s Dilemma)

情况一：假设 A 是真母亲，B 是假母亲

情况二：假设 A 是假母亲，B 是真母亲

蛋糕切分（或和尚分粥）

合租分房间 & 分租金

步骤 1：确定帕累托最优分配

步骤 2：求解无怨价格区间（Envy-Free Zone）

步骤 3：具体定价 —— 平分超额福利

热门标签

激励相容 (IC) 与个体理性 (IR) 的实现：维克里拍卖